

Essay #2: Exploration of Fibonacci Numbers and Related Topics


History:
Medieval mathematician and businessman LEONARD PISANO FIBONACCI or Leonardo da Pisa [Note: two different historical links to the internet] was born and died in Pisa which is now Italy (1170-1250 AD). He traveled extensively with his father, a customs officer in North Africa, to Egypt, Syria, Greece, Sicily, and Provence. About 1200 he returned to Pisa to write a book about mathematics and business that he had learned throughout his travels. In 1202 he published Liber Abaci ("The Book of Calculations") that used arithmetic and algebra to introduce several concepts into Europe.
Fibonacci is credited for two things:
1. Introducing the Hindu-Arabic place-valued decimal system and the use of Arabic numerals into Europe. (Can you imagine us trying to multiply numbers using Roman numerals?)
2. Developing a sequence of numbers (later called the Fibonacci sequence) in which the first two numbers are one, then they are added to get 2, 2 is added to the prior number of 1 to get 3, 3 is added to the prior number of 2 to get 5, 5 is added to the prior number of 3 to get 8, etc. Hence, the sequence begins as
1, 1, 2, 3, 5, 8, 13, 21,34, 55, 89, 144, etc Back in his time, he described the above sequence in the form of a "real-world" problem:
How many pairs of rabbits will be produced in a year, beginning with a single pair, if in every month each pair bears a new pair which becomes productive from the second month on?
(Courtesy of American Rabbit Breeders Association)
Geometric Interpretation of Fibonacci Numbers:
The Fibonacci sequence can be geometrically interpreted by increasingly larger squares of unit dimension. If the number one (1) is added to one (look in the center of the following figure), the result is two - which is the side length of the square annotated with a 2. If squares 1 and 2 are added together, the result is square 3 (side length of 3). The same procedure applies for square 5: square 3 + square 2 (actually squares 1 plus 1). Hence, the Fibonacci sequence can be illustrated by adding squares as described.
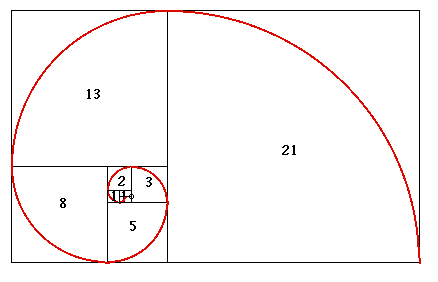
As a bonus, a spiral can be superimposed on
the boxes in the above figure. This spiral approximates the shape
of several spiral shells occurring in nature.
Examples of Fibonacci Numbers Occurring in Nature:
There are several examples. The first is the sunflower arrangement of seeds. There is a Fibonacci number of spirals as you can verify by the following two pictures. Mother Nature arranges the seeds for order and to prevent overcrowding.
 |
 |
Another example is the lineage of the honeybees (similar to rabbits as mentioned by Fibonacci)

and the number of pedals on many different flowers and the occurrence of leaves on many different plants.
Explorations with Fibonacci Numbers:
Using the Excell Spreadsheet (separated into blocks of 10), observe the first 40 terms of the basic Fibonacci sequence in the first column ending with 102,334,155. Recall that this sequence is a recursive sequence which depends on the value of the previous two entries to obtain the next entry. Note that there is no repetition of numbers.




If we compute a ratio of each term with its previous term (as computed in the second column), then the ratio approaches a number accurate to 9 decimal places in the 25th line (but the 24th entry in the sequence of ratios). This convergence can be illustrated by the Microsoft Excell Chart Wizard in the following chart.

If we compute a ratio of each term with the term that is 2 entries earlier (eg, the third term divided by the first term, and so forth), then we can observe the ratios in the third column: "Ratio-Every 2d Term." This ratio converges on a number (accurate to the same 9 decimal places) in the 26th line (24th entry in the sequence of ratios) as illustrated in the following chart:

Similarly, if we view the ratio of each term with the term that is 3 entries earlier (eg, the fourth term divided by the first term), then we can observe the ratios in the fourth column: "Ratio-Every 3d Term." This ratio converges on the 34th line (31st entry in its own sequence of ratios). If this ratio were charted, it would be a very similar chart to the ones, above, with the exception of converging on the value of 4.236067977.
THE GOLDEN RATIO:
An application of the ratios of the Fibonacci sequence is the ratio of two successive terms (the second column in the above table). This ratio converges to a well-known number called phi (in the Greek alphabet) = 1.618033989 (to 9 decimal places).
As background interpretation, if two successive terms in a Fibonacci sequence are described as a and b, then
(b/a) is approximately = (a+b)/b, and
(b/a) is approximately = (a/b) + 1.
If phi (which we will now call x) is the limit of (b/a), then
[Recall: If (a/b) = x, then (b/a) = (1/x).]
Solving for x, we get the quadratic equation
When using the quadratic formula:
which is approximately = 1.618033989 (9 decimal places). This golden ratio is the same ratio the Greek architects used at the Parthenon in Athens where phi is the ratio of the base over the height.

In geometry, the pentagon uses a ratio of the diagonals over the side to be phi. When the diagonals intersect each other, the ratio of one diagonal segment over the entire diagonal is phi. Hence the star that the pentagon produces is called the pentagram and is the same 5-pointed star that is uses on the United States flag and many other flags of the world.

Lucas Sequence:
The Lucas sequence is similar to the Fibonacci sequence except that it has different seed (starting) values of 1 and 3. Hence, the sequence is
as shown in the following chart in the first column:

Notice that in a sequence of 30 numbers that the ratios in the second, third, and fourth columns (as previously described) converge to the same numbers as previously declared.
The only other variation of interest might be to try different seed values of, perhaps, 2 and 5:

Even though the sequence starts off slightly different, exactly the same conclusions can be made about the ratios of one term over the other as observed in the second, third, and fourth columns: the ratios converge to the same numbers as before.
References:
http://mathacademy.com/platonic_realms/encyclop/articles/fibonac.html
http://passmaths.org/issue3/fibonacci
http://arba.net/photo.html
http://www.cyberbee.net/