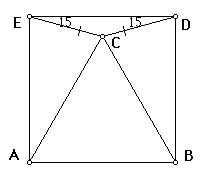
Second Geometric Proof of 15-Degree Problem:
Given: Square ABDE with isosceles triangle CDE constructed within the square in which the isosceles triangle has 15-degree base angles.

Prove: Triangle
ABC is an equilateral triangle.
1. Construct triangle ACI is such a way that angle CAI = 15 (degrees) and AC = CI. Then angle CIA = 15 (degrees).

2. In a similar manner construct triangle BCI where angle CBI = angle CIB = 15 (degrees) and BC = CI.
3. Triangle CDE is similar to triangle ACI ( by construction and by AA Similarity Postulate).
4. Since CI = CI, then triangle ACI is congruent to triangle BCI (AAS Triangle Congruence Theorem).
5. Since AI = BI (corresponding parts of congruent triangles are congruent, CPCTC), then triangle ABI is an isosceles triangle.
6. Angle AIC + angle CIB = angle AIB = 30 (degrees) (Angle Addition Postulate).
7. In isosceles triangle ABI, after subtracting angle AIB (30 degrees) from 180 degrees, there remains 150 degrees which is split between the two base angles. Hence, angle IAB = angle IBA = 75 degrees.
8. Angle CAB = angle IAB - angle IAC = 75 - 15 = 60 (degrees).
9. In a similar manner, angle CBA = 60 degrees.
10. Angle ACB = 180 - (angle CAB + angle CBA) = 180 - (60 + 60) = 60 (degrees).
11. Hence, ABC is an equiANGULAR, isosceles triangle where AC = BC (sides opposite equal angles are themselves equal).
12. ABC can also be shown to be an equilateral triangle as follows. (For the purpose of this latter proof, let us simplify the identification of the angles of equiangular, isosceles triangle ABC by angle A, angle B, and angle C.)
13. Angle A = angle C, and AC = BC (given).
14. BC = AB (sides opposite equal angles are themselves equal).
15.AC = AB (transitive property) and AB = BC = AC.
16. Hence, ABC is an equilateral
triangle . (QED)