F. Klein (1849-1925)
We want to investigate the relationships between altitudes and orthocenters
and their connections with the Nine-Point Circle. Our exploration centers
around two questions:
1. Can we find interesting mathematical phenomena and make connections
among the altitudes and orthocenters of a given set of triangles?
Our exploration begins with the following construction:
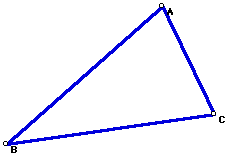
First, construct any triangle ABC.

Next construct the orthocenter, H, of triangle ABC. Recall the orthocenter of a triangle is the common intersection of the three lines containing the altitudes.
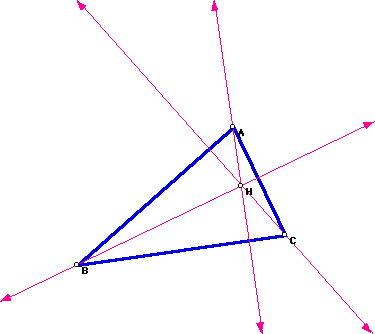
For a GSP script that constructs the orthocenter of any triangle,
click here.
Now consider the triangle HBC. Construct the orthocenter of triangle HBC.
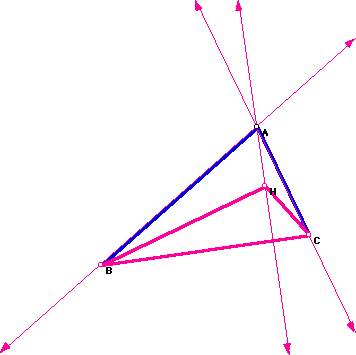
Did you notice anything interesting?
When constructing the orthocenter for HBC, the altitude from H to BC is
the same as the altitude from A to BC. Also, the altitude from B to HC lies
on segment AB, one of the sides of the original triangle ABC. Similarly,
the altitude drawn from C to HB is also segment AC. The most interesting
of all is the orthocenter of triangle HBC is A, one of the vertices
of the original triangle ABC.
Does this same pattern repeat itself when constructing the orthocenters
for triangles HAB and HAC?
If our conjectures are true, then the orthocenter of triangle HAB
should be C and the orthocenter of triangle HAC should be B.
Construct the orthocenters of triangles HAB and HAC, respectively, to verify.
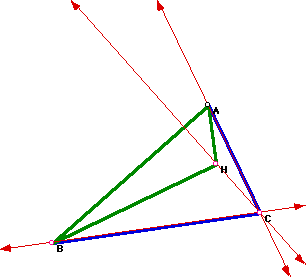
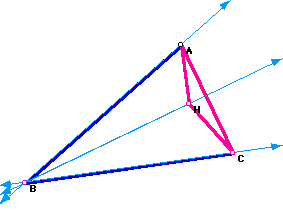
The orthocenter of triangle HAC is B.
Let's also look at what happens when we reverse the order of constructing
the original triangle ABC when the orthocenters for each individual triangle
are constructed from the orthocenter of triangle ABC.
For example, start with triangle HAC.
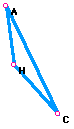
Next construct the orthocenter of HAC call it B.
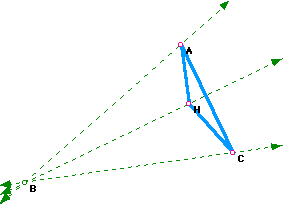
When the orthocenter B is constructed, a new triangle ABC is also constructed in the process where B is a vertex of this new triangle ABC. Furthermore, two more new triangles are formed from this construction, triangles HAB and HBC. If we look at triangle HAB and HBC individually and construct their orthocenters, we would find their orthocenters to be vertices of the triangle ABC. Also the point H, the common vertex of the three triangles HAC, HAB, and HBC, is the orthocenter of triangle ABC.
Why is this true?
Let's look at the case :
If H is the orthocenter of triangle ABC, then A is the orthocenter of triangle HBC.
We are given that H is the orthocenter of triangle ABC. By definition of orthocenter, we have
segment HA is perpendicular to segment BC
segment HB is perpendicular to segment AC
segment HC is perpendicular to segment AB.
Now consider what we are trying to prove that A is the orthocenter of triangle HBC. Let's look at the definition of orthocenter again and apply it here.
If A is the orthocenter of triangle HBC, then by definition the following holds,
segment AH is perpendicular to segment BC
segment AB is perpendicular to segment HC
segment AC is perpendicular to segment HB.
If we compare what we get when we apply the definition of the orthocenter,
we can conclude that the above statements are equivalent. Thereby showing
that if H is the orthocenter of triangle ABC, then A is the orthocenter
of triangle HBC.
Click here for an animation as triangle
ABC varies by shape and size.
As triangle ABC is changing, notice what happens when triangle ABC becomes
a right triangle. H becomes B and their circumcircles overlap. Remember
in a right triangle, the vertex at the right angle is also the orthocenter.
So it makes sense that their circumcircles are the same.
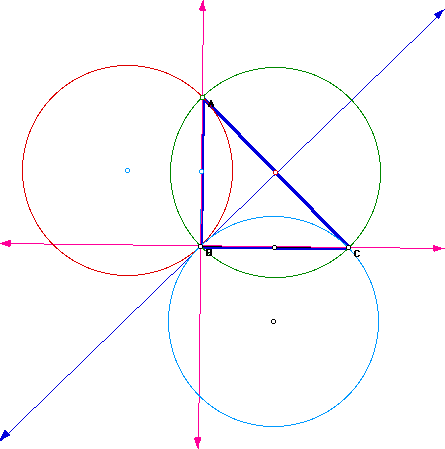
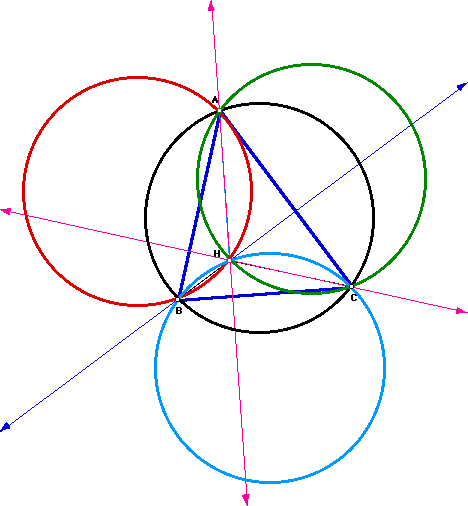
If we continue to push point B further in towards segment AC to make an
obtuse triangle, the orthocenter shifts from inside triangle ABC to outside
of the triangle where the altitudes meet. Remember in an obtuse triangle,
the orthocenter always lies outside of the triangle.
Why? The intersection of the extended altitudes intersect outside of the triangle.
What will happen if we continue pushing B further in until it lies on segment
AC?
Click here for an animation as B moves
closer to segment AC.
When point B moves so close that it lies on segment AC and triangle ABC
no longer exists, the following occurs.
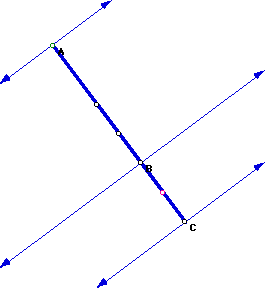
Notice points A, B, and C are all on one segment and the altitudes have
been transformed to perpendicular lines to segment AC through the points
A, B, and C.
Recall the Nine-Point Circle of any triangle
passes through the three mid-points of the sides, the three feet of the
altitudes, and the three mid-points of the segments from the respective
vertices to the orthocenter.
The center of the Nine-Point Circle is the midpoint
of the segment whose endpoints are the orthocenter and the circumcenter.
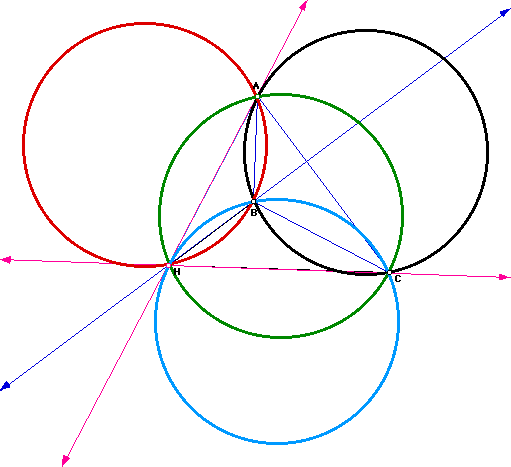
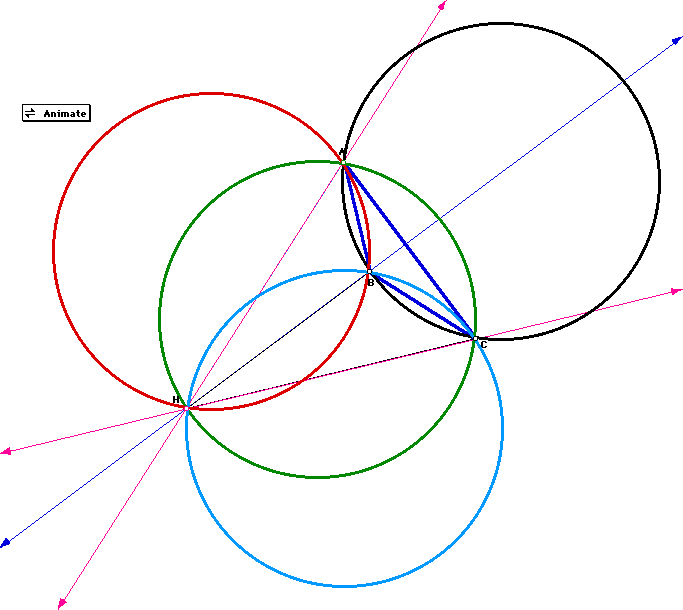
For fun, construct the Nine Point Circles for each triangle
ABC, HAB, HBC, and HAC.
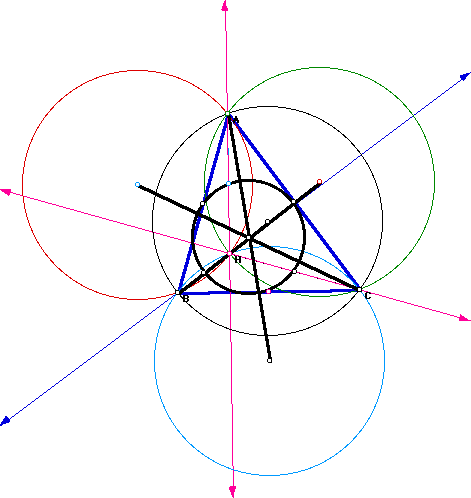
What do you discover?
Most fascinating, the Nine-Point Circles for all four triangles are the
SAME.
The center for the Nine-Point Circles is the midpoint of the segment
whose endpoints are the orthocenter and the circumcenter. The center of
the Nine-Point Circle also lies on the Euler Line. The Euler line
is the line containing the centroid, circumcenter, and orthocenter of a
triangle.
As triangle ABC moves and changes shape and size the Nine-Point Circles
still remain the same for triangles ABC, HAB, HBC, and HAC.
Click here for an animation.
Constructing the Nine-Point Circle for the triangles ABC, HAB, HBC, and
HAC is a nice extension that ties together the concepts of altitude, orthocenter,
centroid, Nine-Point Circle, and the Euler Line. The construction stresses
the interrelatedness of all these geometrical concepts.