PEDAL TRIANGLES and the Nine-Point Circle |
| Alone at nights, I read my Bible more and Euclid less. |
Robert Buchanan (1841-1901)
(An Old Dominie's Story)
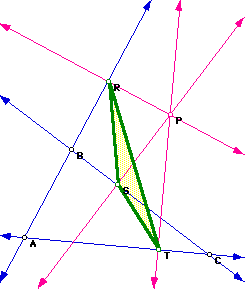
Let triangle ABC be any triangle. If P is any point in the plane, then
the triangle formed by constructing perpendiculars to the sides of ABC (extended
if necessary) from P, where points R, S, and T are the intersections, is
called the Pedal Triangle.

Triangle RST is the Pedal Triangle for Pedal Point P.
Click here for a GSP script to construct
a pedal triangle where P is any point in the plane of ABC.
Click here for a GSP animation for
various locations of point P.
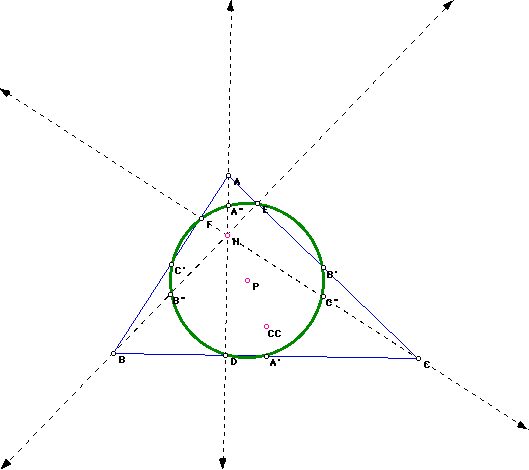
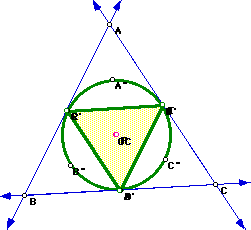
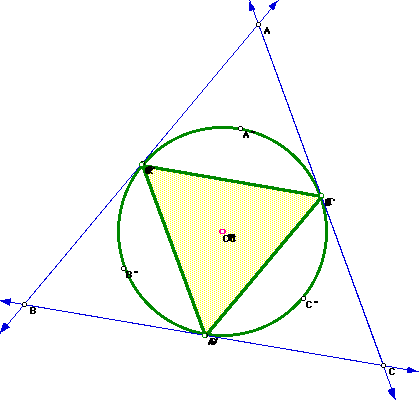
Now, construct the pedal triangle RST using the center, P, of the nine-point
circle for triangle ABC as the pedal point.
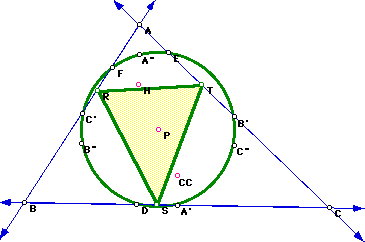
Will the pedal triangle RST ever lie on the Nine-Point Circle?
Yes! Notice the Pedal Triangle RST will lie on the nine-point circle
when the circumcenter, CC, orthocenter, H, and the pedal point, P, all are
the same point; that is, when the circumcenter and the orthocenter become
the center of the nine point circle, also known as P.
Here are a few examples: