
The Lidless Box
by Jamila K. Eagles
Consider a rectancular sheet of cardboard 15 in. by 25 in. Using GSP
we will use the scale 15= 1.5 and 25 = 2.5If a small square of the same
size were cut from each corner and each side folded up along the cuts to
form a lidless box. First consider the sheet of cardboard:
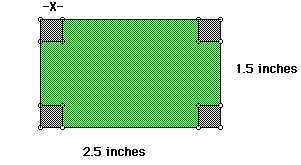
After folding along the cuts of each x by x the square, we will have
the following:
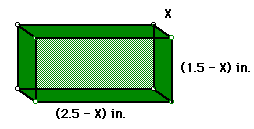
We have a lidless box with dimensions: l = 2.5-x, w= 1.5-x, and height
= x.
Using Geometer's Sketch Pad we can change the dimensions of our box
in order to find the maximum volume.
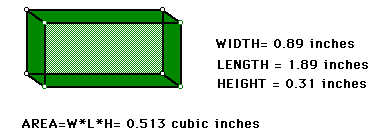
This can be found by changing the size of the square cut from each corner.
I observed the volume as I increased the size of the square. After 513 cubic
inches, the volume began to decrease, so I concluded that 513 cubic inches
is the maximum volume of the box.
The next question, what size(s) of the square will produce a box of volume
400 can be found in a similar way.

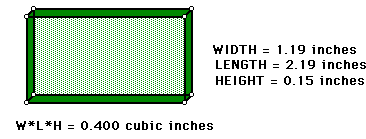
In the two figures It is easy to see that the box will have volume 400 with
two different sets of measures, meaning with two different sizes for our
square.
Using GSP gives an advantage to the exploration because it provides a visual
explanation, but as you can tell from the figures above it is sometimes
hard to get an exact measurement, so we will try another approach to answer
the same questions.
Using Algebra Expressor, can use the formula A=l*w*h and substitute
in order to find our equation. We know the values for l, w, and h, and it
follows that our formula is {A = x(25-x)(15-x)}. The graph follows:

Algebra Expressor allows us to zoom in on certain points, let's
begin by finding the maximum
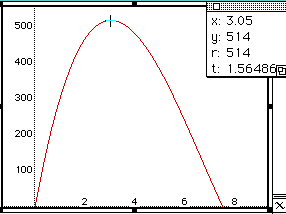
By the graph, the maximum value is 514 and this occurs when x has the
value of 3.05. Now let's try to find the value of x when the volume is equal
to 400.

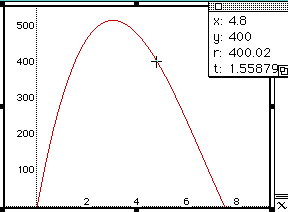
These graphs show that the volume of the box is 400 when the value of
x is 1.4 and 4.8.
Finally we can look at this problem with the help of a spreadsheet program.
I am going to use Microsoft Exel. We can begin by entering the values for
x in one column and our formula for the volume in the second column. We
observe the data to find our maximum volume.

This tells us that our maximum value occurs somewhere around 3. We can
look closer at the area around 3 and see a more exact measure of our volume.

Finally, we can use the spreadsheet to find the values of x when the volume
is 400.
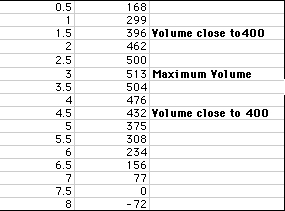
We can find more exact values by looking closer at the region around
the values x=1.5 and 4.5. Looking closer around 4.5 we have the following.
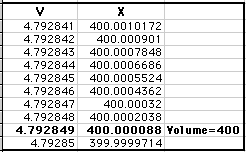
The same procedure can be done to find a more exact value around 1.5.
Using different software, a maximaization problem can be solved in many
ways. These concepts give a visual aspect, a graphing perspective, and a
formula perspective.
Return to Finals page
Return to Jamila's page














