Triangle Ratios
By Jamila K. Eagles
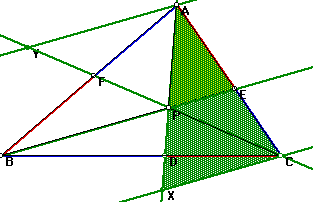
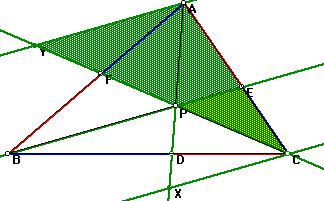
Given trriangle ABC and an arbitrary point P inside the triangle draw
lines AP, BP, and CP extended to their intersectionswith the opposite sides
in points D, E, and F respectively.
Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various
locations of P.
From my exploration I conclude that (AF)(BD)(EC)=(FB)(DC)(EA) for the triangle.
I will begin my proof by drawing a set of parallel lines to find similar
triangles.
Drawing lines AY and CX gives us our first set of similar triangles. These
triangles are similar by the theorem AA which states that if two angles
of two triangles are equal, then the triangles are said to be similar triangles.
I used the fact that vertical angles are congruent, and the fact that if
two parallel lines are cut by a transversal, alternate interior angles are
congruent. Therefore, BPD is similar to CXD, and 
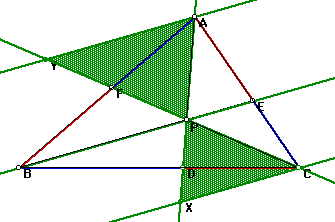
The next two sets of triangles follow the same reasoning:
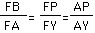
Next I used the fact that if two triangles have one common angle and
one of the sides of one triangle is parallel to the side of the other triangle,
then the sides are proportional. Therefore triangle AXC is similar to APE
and the same reasoning applies for triangle CYA is similar to triangle CPE.
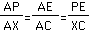
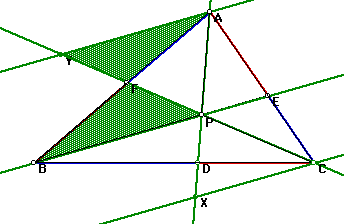
I want to show that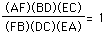 
in order to prove that
We want to show that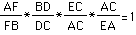 
and by substituting our known values
we now have
and therefore,