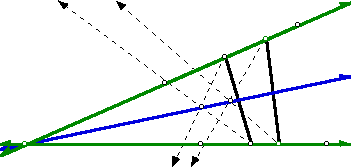
Problem: Imagine a sheet of paper with two line segments drawn on it, as shown. Without extending the paper or the line segments, construct the bisector of the angle determined by the two line segments.

We can begin by using facts that we know about angle bisectors. We know that angle bisectors of a triangle are concurrent. Therfore we can begin our construction by creating the base of a triangle that would have a vertex where these two lines will meet.

Now we can construct the two known angle bisectors. The point of intersection will be a point on the angle bisector we wish to construct.

Since we only need two points to construct a line, we can repeat this construction with another segment that will also be the base of a triangle that has a vertex where the given segments meet.

We now have two points that lie on our angle bisector, and we can successfully construct it.

If we extend the given segments, we can check our solution.