The Circular Window
We can begin constructing our window by constructing an isosceles triangle.
We can now use the vertices of our triangle as the center of our three circles. We know that we want each of the three circles to meet at one point only. We can get this by constructiing the circles that go through the midpoint of the side of the triangle.
We now have our three tangent circles that are a part of our circular window. Our next step is to construct a circle around each circle in such a way that it is tangent to each of the three circle. If we construct angle bisectors of the triangle, each angle bisector intersects one of the smaller circle. It is clear that this point of intersection is equidistant from the incenter of the equilateral triangle. Therefore, we can construct a circle that has a center that is the incenter of the triangle and the radius of a segment connecting the center and the point of intersection of the angle bisector and the smaller circle.
We now have the circles that form this circular window. We can complete the window by erasing the unwanted arcs.
We can explore this construction to find the area of the bounded region. If we look back at the construction we notice that we have an isoceles triangle that goes through each of the smaller circles.
. When we drop
an altitude we can find the height because we now have a 30-60-90 triangle
with leg=r and hypotenuse=2r. This will give us a leg of (sqrt 3)r which
is our height. Therefore, we have the area of our triangle is 
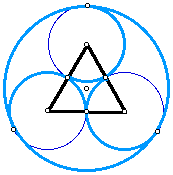
Next, we can find the area of each sector within the triangle. We know
that each one is 
. If we multiply this by 3 we have 
Thus the area
of the three sectors within our isosceles triangle is 
.
To find the area of the bounded region in our window we can simply subtract the area of the sectors from the area of the triangle. This area is represented by.
