Assignment 2 , Problem # 6
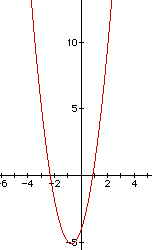
Graph 
i. Overlay a new graph replacing each x by ( x - 4).
ii. Change the equation to move the graph into the second quadrant.
iii. Change the equation to produce a graph concave down that shares the
same vertex.
Overlaying a new graph by replacing each x with (x-4) gives us the equation
and the graph is represented by the green parabola below.
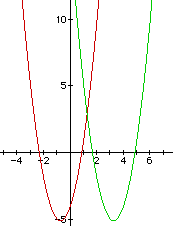
We can see from the graph that replacing each x with (x-4) shifts the
graph 4 places to the right. So replacing x with (x- a) , where a is any
real number gi ves us a horizontal shift (a) spaces to the right or left.
Now we must try to change the equation so that the graph appears in the
second quadrant. Using the information fron the last demonstration, we know
that changing x to (x-a) will shift our graph horizontally and since we
want to shift our graph to the left, we choose a = -4. Now we need to determine
what is needed to shift the graph up and down. Let's try replacing y with
(y - b). Since the graph is at y = -5, and we want the graph to shift above
y = 0, we choose b = 6. Changing the equation we now have 
.
The graph is shown below in blue. For -6 < y < 12 the graph of our
new equation appears in the second quadrant, but it should be known that
for some larger value of y our new graph crosses the y axis.
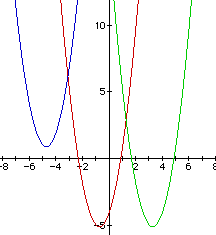
Finally , we must change the equation to produce a graph concave down
that shares the same vertex. First we know that if we have an equation of
the form 
, the sign of c determines if the parabola is concave upward or downward.
Using our equation we can complete the square to get an equation
of this form. By completing the square, we get the equation 
. Now to make
this parabola concave
downward we simply change the sign of 2. So our new equation is 
,
and the graph is represented by the green parabola below.
