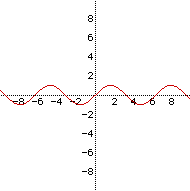
The graphs of functions defined by y = sin x are called sine waves
or sinusoidal waves. Notice that the graph repeats itself as it moves along
the x-axis. The cycles of this regular repeating are called periods. This
graph repeats every 6.28 units or 2 pi radians. It ranges from -1 to 1;
half this distance is called the amplitude. So the graph below has a period
of 6.28 and an amplitude of 1.
We will investivage different values for the amplitude and period as well
as phase shift which appears to set the graph at a different place on the
x axis.

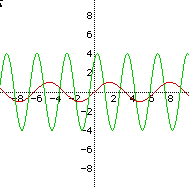
Let's look at what happens to the graph with different values of a. On
the left below is x= 2 sin x and y = 6 sin x on the same graph
with y = sin x. Notice how high and how low the graph goes; this
is called the range. What do you think will happen when the sign of a
is changed to a negative? Look at the graph on the right below to see y
= -3 sin x and y = -5 sin x on the same graph with y = sin
x. What happens to the graph as a changes?
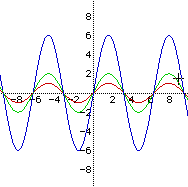
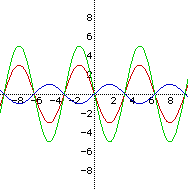
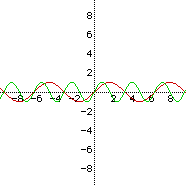
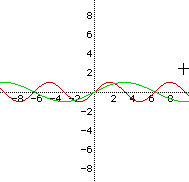
Look again at the equation y = a sin (bx + c). Notice that we
have varied a, the amplitude, and b, the period. The last
variation in this equation will be c. In the first equation, y
= sin x, c is equal to zero. Look at the graph on the left to
see that curve as well as the curve of the equation y = sin (x + 2).
Notice that the new curve is shifted two units to the left of the original
one. See the graph on the right to find out what happens when y= sin
x is overlaid by y = sin (x-3). Can you see that the graph is
shifted three units to the right? Make a conjecture about variations of
c.