OBJECTIVES:
Students will be able to :
1) define various terms associated with circles
2) determine the area of a given circle
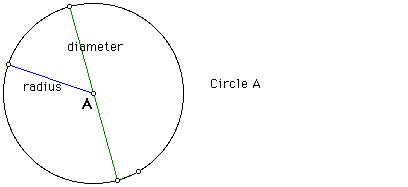
A circle is the locus of points in a plane equidistant from a given point.
That point is the center of the circle. A circle is named by its center.
A radius of the circle is a segment from the center to any given point on the circle.
A diameter is a segment that contains the center of the circle and has endpoints on the circle.

In lesson # 1, the distance around a polygon is its perimeter. The distance around a circle is its circumference.
Click here for a GSP sketch to discover the relationship between the circumference and diameter.
From your discovery, you should have found that the ratio was always the same number. Since this ratio is always constant, it was given a Greek letter to represent it in problems. The number pi is the ratio of the circumference of any circle to its diameter.
This ratio = c/d is an irrational number. It has an approximate value of 3.1415926..... or 3.14.
Using this ratio, the circumference of a circle is the product of pi and its diameter d, or to approximate, C = (3.14)d.
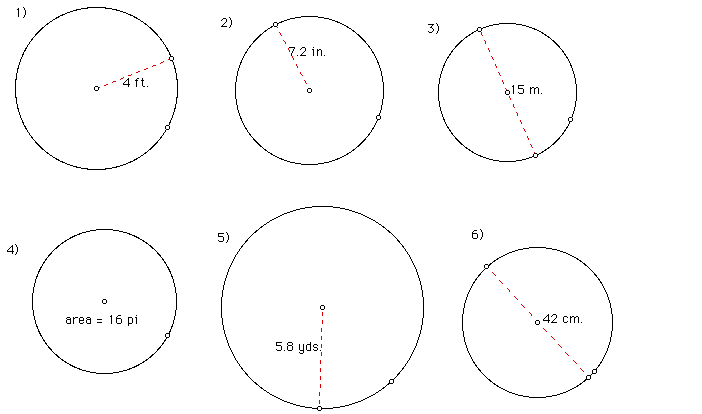
Circumference Practice:
Find the circumference of the following circles:
Click here to check circumferences.
The area of a circle is the product of pi and the square of its radius, r, or
Area Practice:
Find the area of the following circles:

Click here to check your answers.
Now consider a circle with a radius r units inscribed in a square. What is the length of each side of the (blue) square? What is the ratio of areas of the circumscribed square to the circle?

What is the length of each side of the square inscribed in the circle?