Assignment 11
Polar Equations
by Kelli Nipper
Rose Curves
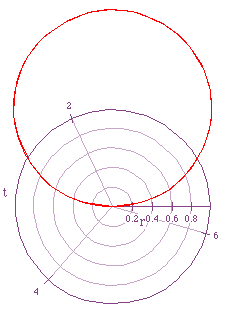
Consider the equation r=2a sin (kt) when k is constant at 1 and a is
varied. The following graphs shows the graphs for values of a=1/2,-1/2,-1,1:
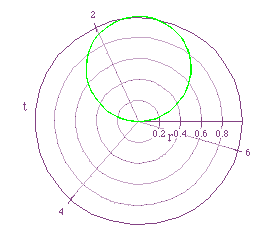


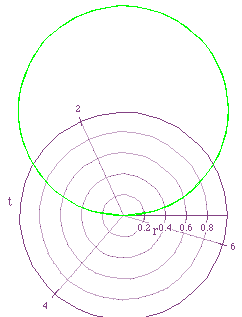
The equation produces a circle with radius of absolute value of a and
center at (0,a).
Varying k when a is constant produces 2 different behaviors:

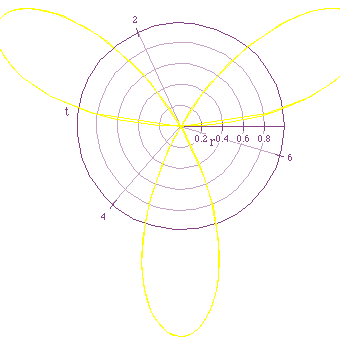

If k is odd, the rose has k petals.
If k is even, the rose has 2k petals.
Considering the same equation replacing sin t with cos
t:
The same relationships exist, the only difference being that the rose
is rotated pi/4 radians.
Limacons
Consider the equation r = 2 sin (t) + b [for b = 1, 2, 3]:
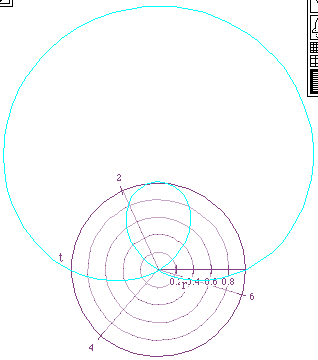

When b=1, or any b/2a < 1, a limacon with an inner loop is formed.
When b=2, or any b=2a, a special case limacon is formed called the cardiod.
When b=3, or any 1 < b/2a < 2, a limacon with a dimple is formed.
When b=4, or any b/2a > or = 2, a convex limacon is formed.
Considering the same equation, replacing sin t with cos t:
The same relationships exist, the only difference being that the limacon
is rotated pi/2 radians.












