Orthocenter

Consider what happens with the position of the orthocenter when the triangle is right, obtuse, or equilateral.

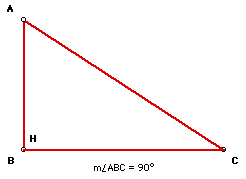
Location for right triangles:
When the triangle is right, the orthocenter is the vertex of the triangle and the right angle. (Since this is where the two legs are altitudes.)

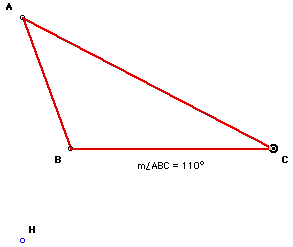
Location for obtuse triangles:
When the triangle is obtuse, the intersection of the altitudes is outside the triangle.

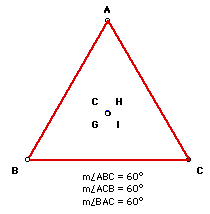
Location for equilateral triangles:
When the triangle is equilateral, the orthocenter is located at the same position as the centroid, circumcenter, and incenter.

---

Click Here to use a GSP script for the construction of the orthocenter.

---

Return to Write-Up 4 (Centers of a Triangle)

---

Return to Write-Up 8 (Altitudes and Orthocenters)

---

---