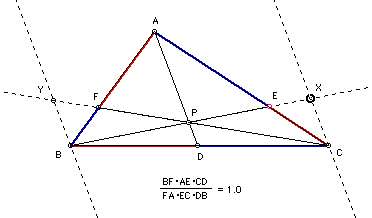
Given any triangle ABC and an arbitrary point P
in its interior. Extend segments from each vertex through P to intersect
the opposite sides, giving the segments AD, BE, and CF.
Explore (AF)(BD)(CE) and (FB)(DC)(EA) for various triangles
and various locations of P.
Form the Ratios:
Prove that :
The approach here will be to construct auxiliary lines
so that similar triangles can be found that allow substitution for the ratios.
The Angle-Angle Theorem, as well as the properties of parallel
lines intersected by a transversal, are necessary to prove the similarity
of triangles created by constructing these auxiliary lines.
Construct a line through Point B and C parallel to AD. Extend BE to intersect at X and CF to intersect at Y.
Vertical angles and alternate interior angles created by
the parallel lines (AD, YB, XC) give us similar triangles APE and
CXE as well as triangles APF and BYE.
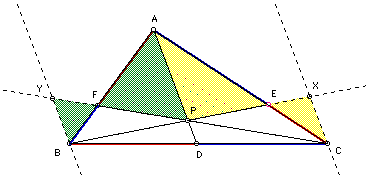
Therefore:
__________________________________________________________________
Other similar triangles are created by the auxiliary lines.
As seen below, they have parallel bases and share one vertex.
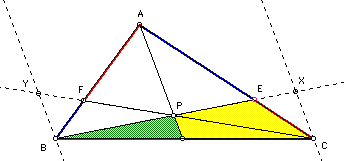
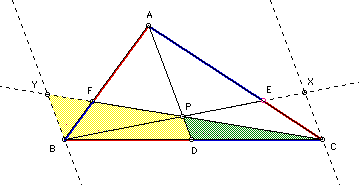
Therefore:
From these 4 sets of similar triangles, the following corresponding
ratios can be used for substitution:
Thus:
Because:
__________________________________________________________________
Return to Final Exam Page
__________________________________________________________________
Return to Kelli's Class Page