 refers
to a geometrical problem of antiquity. The problem was if you were given
a circle of known area, could you create a square of the same area using
only a compass and straightedge.
refers
to a geometrical problem of antiquity. The problem was if you were given
a circle of known area, could you create a square of the same area using
only a compass and straightedge.
Problem of Antiquity leads to
Lunar Discovery
by
Mike Patterson
"Squaring the Circle"
or "Quadrature of the Circle"
-  refers
to a geometrical problem of antiquity. The problem was if you were given
a circle of known area, could you create a square of the same area using
only a compass and straightedge.
refers
to a geometrical problem of antiquity. The problem was if you were given
a circle of known area, could you create a square of the same area using
only a compass and straightedge.
"One of the earliest Greek mathematicians to  attempt
to treat the problem of the "quadrature of the circle" in pure geometric
form, with the specific restriction that only compass and straightedge
should be used, was Hippocrates of Chios (440 B.C.) He was able
to show that the area of certain lunes (cresent-shaped figures formed by
two intersecting arcs) could be represented exactly by trianglular (and
hence rectangular) areas. For example, if AOB is a quadrant of a circle
and AB is the diameter of a semicircle lying outside the quadrant, then
the lune bounded by the semicircle and the quadrant has the same area as
triangle AOB. His success with such special cases led him to suppose that
he could eventually draw a polygon and hence a square whose area is exactly
that of a circle." (P150 NCTM Yearbook #31)
attempt
to treat the problem of the "quadrature of the circle" in pure geometric
form, with the specific restriction that only compass and straightedge
should be used, was Hippocrates of Chios (440 B.C.) He was able
to show that the area of certain lunes (cresent-shaped figures formed by
two intersecting arcs) could be represented exactly by trianglular (and
hence rectangular) areas. For example, if AOB is a quadrant of a circle
and AB is the diameter of a semicircle lying outside the quadrant, then
the lune bounded by the semicircle and the quadrant has the same area as
triangle AOB. His success with such special cases led him to suppose that
he could eventually draw a polygon and hence a square whose area is exactly
that of a circle." (P150 NCTM Yearbook #31)
In 1882 Ferdinand Lindemann, modelling his proof after Hermite, proved that pi, also, is a transcendental number. No transcendental number is constructible, therefore Lindemann's result settled the famous problem concerning the possibility of "squaring the circle". (P84 NCTM Yearbook #31)
Does the Lune = Triangle?
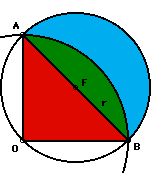 |
Red
Section
Area of the triangle
|
Red
+ Green Section
Area of the quarter of the circle with radius OB
|
| Green
Section
Red + Green - Red = Green
|
Blue
+ Greem
Section
|
Blue
Section
Blue + Green - Green = Blue
|
| Does the Lune
= Triangle? Yes.... |
||
This finding gave Hippocrates great hope that he would be able to square the circle, in that a right isosceles triangle is simply one half the area of the square. Unfortunately it didn't happen as he had invisioned. He continued to pursue shapes that he could square such as triangles, rectangles, pentagons,.....
"Squaring the Rectangle"
In an attempt to "square the circle" Hippocrates found a way to "square" a number of other shapes, one of which was the rectangle. Hippocrates' approach was to a special similar triangle relationship.
 |
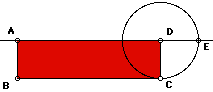 |
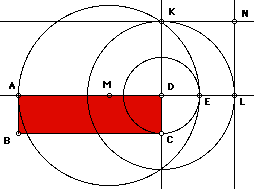
| Given any rectangle ABCD with area = (AD)(DC) | Construct a circle centered at D with radius DC. E is the point of intersection of AB extension and the circle. Note DE = DC, this relationship become important later. |
 |
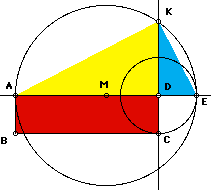 |
| Construct a circle with a diameter of AE, and center at M, the midpoint of AE. | K is the intersection of the perpendicular line through D and the circle centered at M. |
 |
The yellow
triangle and blue triangle are similar by
construction. Thus:
|
 |
 |
|
|
|
"Squaring the Triangle..the Trapezoid...the Pentagon..."
Following a similar pattern as above, one is able to square a number of shapes. Simply divide the shape into triangles, and then into a rectangle, and then square it. If I can do it, so can you!! For the sake of time and space, I will simply provide a picture representation of my work!!
 |
 |
 |
|
The Ratio Question!
Further investigation and research has found that there are exactly 5 ratios of lunes that are "squareable". "Let 2a and 2b be the angles subtended by the arcs of the lune with respect to the centers of their respective circles. Constructions for the cases a:b = 2:1, 3:1, 3:2, 5:1, and 5:3, are the only ratios that establish squareable lunes by elementary methods" (Scriba, Christoph H.)