 |
 |
 |
 |
Specifically, the Centroid Search works as follows: you enter either a site address or parcel number for your subject property along with your criteria for comparable sales and the width of the area you wish to search. The Centroid Search then uses the property's x,y coordinates and searches a square area around that property for comparable sales meeting your criteria. The search area can be from 0.4 to 6.0 miles in width for the Custom Comparable Report. The Standard comparable Report automatically searches an area 1 mile in width.
If no x,y coordinates are available for the Standard Comparable Report, the search for comparable sales is done by APN (Assessor's Parcel Number) Book and Page. In these cases the search encompasses an area including approximately 1000 - 2000 properties. Therefore, depending on population density, the search area may be more or less than a mile from the subject property.
In some rare cases where no x,y coordinates are available, APN Book and Page recordings may NOT be geographically based. In these instances, a search for neighborhood sales will not be possible with the Standard Comparable Report.
When no x,y coordinates are available for the Custom Comparable
Report, the search for comparable sales is conducted using one of the following
methods: APN Book and Page, tract number or zip code. 
* These distances apply only to the Custom Comparable
Report. The Centroid Search area for the Standard Comparable Report is
1 mile.
Return to Centroid of
Quadrilateral
Introduction
to Spectral Centroid
The spectral centroid of a sound is the midpoint of the
spectral energy distribution of that sound. One might also think of it
as the "balance point" of the spectrum. For this reason centroids are sometimes
displayed as a "fulcrum" underneath a spectral plot. A figure illustrating
the centroids of two simple spectra is shown below.
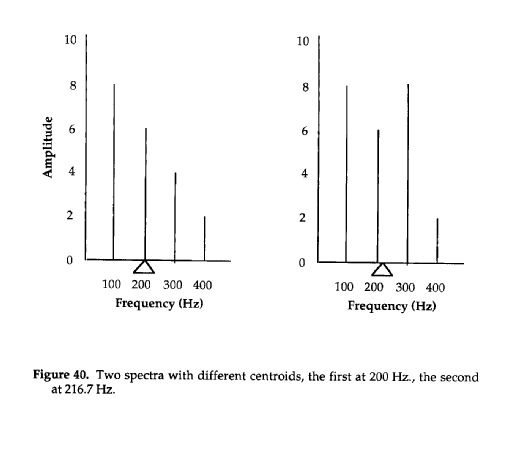
Calculating Centroid - Centroid is calculated by taking the sum of the frequencies weighted by (i.e. multiplied by) the linear amplitudes, divided by the sums of the linear amplitudes alone. This could be programmed in C as follows:
for (i = 0, den = 0.0, num = 0.0; i < N; i++)
{num += amps[i] * freqs[i]; den += amps[i];} return(num/den);
The calculation for the first spectrum in the example above is
(8*100 + 6*200 + 4*300 + 2*400)/(8 + 6 + 4 + 2)
...while the second is calculated as
(8*100 + 6*200 + 8*300 + 2*400)/(8 + 6 + 8 + 2)
Return to Centroid of
Quadrilateral
Cross
Section & Centroid of a Shape
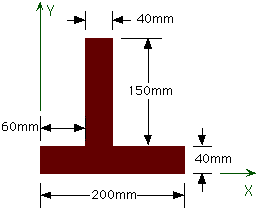
Determine the cross sectional area and centroid location of the structural shape. Note that the centroidal location need not lie on the shape. If the tension stress was 5N/mm^2 , what would the total force in the member be?
 |
a)
b)
c) |
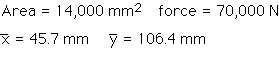
|
|
|
||
 |
 |
| Part | b (mm) | h (mm) | Area (mm^2) | X^ (mm) | Y^ (mm) | X^(area) * 103 (mm^3) | Y^(area) x 103 (mm^3) |
| 1 | 200 | 40 | 8,000 | 100 | 20 | 800 | 160 |
| 2 | 40 | 150 | 6,000 | 80 | 115 | 480 | 690 |
| = | 14,000 | 1,280 | 850 |
Return to Centroid of Quadrilateral