Consider a rectangular sheet of cardboard 15 inches by 25 inches. If a small square is cut from each corner and each side folded up along the cuts to form a lidless box. I am using an automatic drawer (GSP) to draw a box and demonstrate the problem.



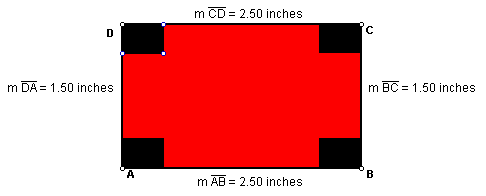
The area in red is the area of the cardboard after the squares have been removed from the sheet. If we were to write an equation for the volume, we would get the following: Volume = (15-2x) * (25-2x)*(x), where x is the side of the squares removed.

Now, let's graph the volume with relation to the variable x.

  After analyzing the graph, students should be able to tell that the maximum volume occurs around 510 and the x value is about 3. Let's zoom into the graph and clarify where the maximum occurs.

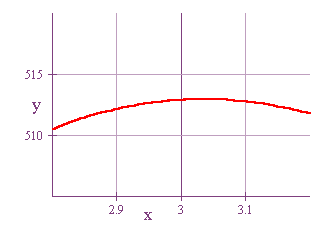
 After zooming in on the maximum point, we can see the maximum occurs at volume = 513 inches³ and the size of square is about 3.2 inches. To find maximum points of an equation, a student needs to take the derivative. The derivative of the Volume equation is

 After taking the derivative, set the equation equal to zero and solve. The solutions are 10.3 and 3.03. However, 10.3 is not a reasonable answer because it lies outside the range. Analyze the original graph, for what values of x is the volume equal to 400? The value of x is about 1.5.

 We will approach this problem using a spreadsheet application. First, let's set up the spreadsheet. Column A will be the variable x, which is the length of the square you are cutting out of the sheet. Column B calculates the longest side of the box and column C is the shortest length of the box. Finally, column D calculates the Volume of the box. Notice, after x = 7 the volume is negative. This shows the limit of the shortest side of the cardboard. Look at the values for volume. The maximum volume occurs at 3.

 

Square	Length	Width	Volume
(x)	(25 - 2x)	(15-2x)
1	23	13	299
2	21	11	462
3	19	9	513
4	17	7	476
5	15	5	375
6	13	3	234
7	11	1	77
8	9	-1	-72

 

Let's now look closer at the values around 3.

Square	Length	Width	Volume
(x)	(25 - 2x)	(15-2x)
3.00	19.00	9.00	513.00
3.01	18.98	8.98	513.03
3.02	18.96	8.96	513.04
3.03	18.94	8.94	513.05
3.04	18.92	8.92	513.05
3.05	18.90	8.90	513.04
3.06	18.88	8.88	513.02
3.07	18.86	8.86	513.00

The data agrees with the graph above. The maximum value occurs at x = 3.03 or 3.04.

 We can also use the graph at the beginning of this exploration to find the value of x when the volume is 400 cubic inches. The x value is about 1.5. Let's use Excel to show where the solution occurs.

 

Square	Length	Width	Volume
(x)	(25 - 2x)	(15-2x)
1.50	22.00	12.00	396.00
1.51	21.98	11.98	397.61
1.52	21.96	11.96	399.22
1.53	21.94	11.94	400.80
1.54	21.92	11.92	402.38
1.55	21.90	11.90	403.95
1.56	21.88	11.88	405.50
1.57	21.86	11.86	407.04

The spreadsheet shows that the solution occurs between 1.52 and 1.53. Let's continue using the spreadsheets to find the solutions by changing the x coordinates to 5 or 6 decimals.

 

1.524926	21.950148	11.950148	399.999553
1.524927	21.950146	11.950146	399.999712
1.524928	21.950144	11.950144	399.999871
1.524929	21.950142	11.950142	400.000030
1.524930	21.950140	11.950140	400.000189
1.524931	21.950138	11.950138	400.000348
1.524932	21.950136	11.950136	400.000507
1.524933	21.950134	11.950134	400.000665
1.524934	21.950132	11.950132	400.000824
1.524935	21.950130	11.950130	400.000983

 

The closest value to 6 digits is 1.524929. Excel is able to give you a more exact answer than a graph.

 

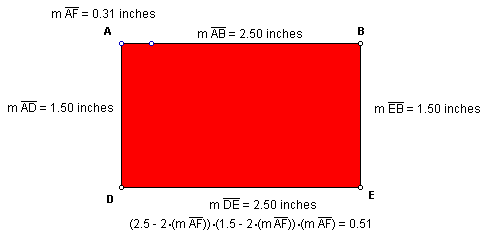
You can use GSP to solve this problem, but it is more difficult. First, construct the polygon and measure all the sides. Next, construct a segment you will vary to determine the length. Below, line segment AF is the segment that represents the square we will cut out. Then, derive a formula to calculate the volume of the lidless box. Vary the length of AF to determine the maximum volume. I used 2.5 and 1.5 inches instead of 25 and 15 to save space.

 

 
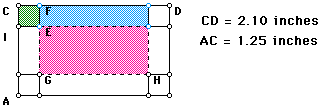
Another approach is actually animate the box to give the full 3-D effect. First, I constructed a sheet using GSP that has the dimensions 2.10 by 1.25. Below, you will find a copy of the sheet.

Now, I would like to constuct the box that coincides with the sheet above. Below, you will find not only the box but the dimensions of the box.

The next logical step to this problem is to use the animation feature of GSP to animate the different values of x and calculate the volume of the box. If you animate the box slowly, it will be apparent which value of x that the maximum volume occurs.

Click Here to see the animation.

The maximum volume (.30 inches cubed) of the box occurs when the segment EF is .28 inches.

I hope this exploration shows you several different tools you can use to solve the same problem. Which one are you more comfortable using? Or do you have any other suggestions we could do?

 View other Final Documents

Return to Kelly Pierce's Home Page

 

Email Kelly Pierce