The circumcenter (c) of a triangle is the point in the plane equidistant from the three vertices of the triangle. Since a point equidistant from two points lies on the perpedicular bisector of the segment determined by the two points, C is on the perpendicular bisector of each side of the triangle. Below is triangle ABC and its circumcenter:

 This write-up explores different locations of the circumcenter for various shapes of triangles.

 

First let's start this exploration by looking at the hierarchy for triangles:

 

 

To begin, construct a scalene (no sides equal) triangle and its circumcenter.

 

 

  

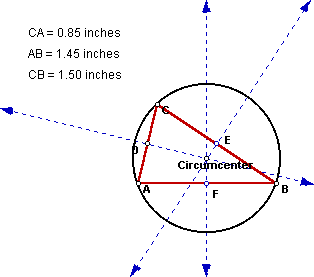
The circumcenter of this scalene triangle lies inside the triangle. Are there any ratios that are important? Let's see what the ratio would be of the distance from the circumcenter to the perpendicular bisector of each side and the length of each side.

  

After analyzing the data, there does not seem to be any relationship between the two distances except that they are all not equal (like a scalene triangle). What if I draw an isosceles triangle? Do you think there will be a relationship there?

 

 The two side of the triangle equal are line segments AB and CB. The distance from the circumcenter to the lines segments AB and CB are also equal. Therefore, their ratios are equal.

 

Do you think an equilateral triangle will have the equal ratios?

 

 

  

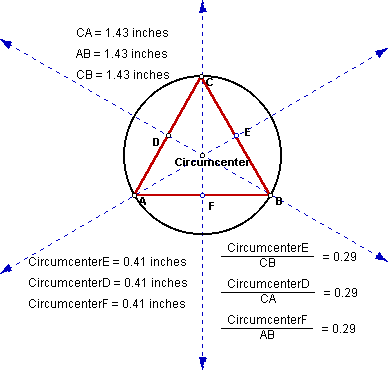
Our predictions are correct. The isosceles triangle has equal distances from the circumcenter to the perpendicular bisectors of each side. Do you think there is any other location of the circumcenter where the distance from the circumcenter to the sides of the triangles are equal? Below is such a case. The points of the triangle appear to form a straight line and all are equidistant from the circumcenter. You cannot draw the circumcenter, because they it lies off the screen.

 

 

 

The circumcenter is 96.24 inches from the perpendicular bisectors. This leads us to another area to explore. What if the circumcenter lies outside the triangle?

Yes, when the triangle is an obtuse triangle (that means one angle is greater than 90 degrees). The above triangle includes an angle with the measure equal to 108 degrees, but also has two equal sides. This also means the distance from the triangles circumcenter to the perpendicular bisector of the equal sides are equal. Does this mean that when a triangle is acute the circumcenter lies inside triangle ABC?

 

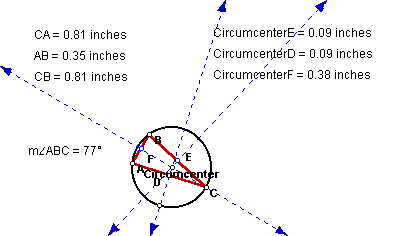
The above triangle has an angle of 77 degrees and the circumcenter lies inside the triangle. What do you predict would happen if the triangle is a right triangle?

 

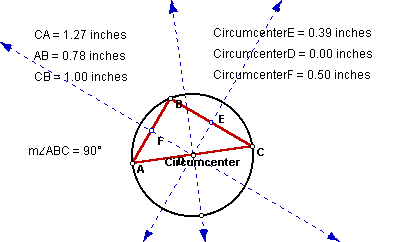
The circumcenter lies on one side of triangle ABC. To continue this exploration, I wanted to look at the 90 degree angle and the side that contains the circumcenter.

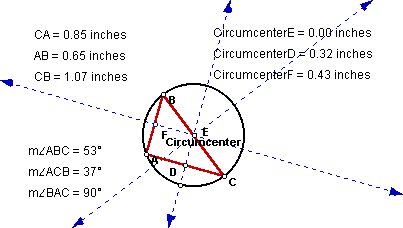
 The side opposite of the angle that forms the 90 degree angle is the one that contains the circumcenter. Let's revisit the obtuse angle problem above. Can we try to conclude anything about the location of the circumcenter with respect to the angle size?

 

If the angle is obtuse, then the side of the triangle that is opposite the obtuse angle lies closer to the obtuse angle. Thus, the circumcenter lies outside of the triangle.

 

This write-up explored all three different classifications of triangles and the different angle types associated with triangles.