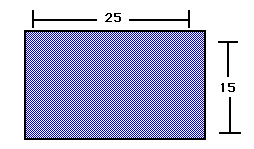
Then we will cut a small square of the same size from each corner
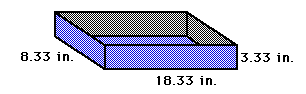
and fold each side up along the cuts to form a lidless box.
Since Volume = length * width * height , we can multiply the lengths of the two sides times the height to find the volume. GSP will measure the lenth of each side by simply selecting the side and choosing the 'Measure - Length' tool. We can then use the calculator that GSP provides to compute the volume. So,
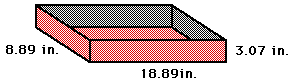
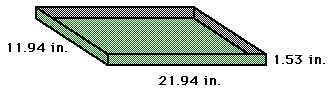
For the second size, the estimation is not as close. So, we the nearest value below 400

and the nearest above 400 in order to obtain an approximation of the sizes.
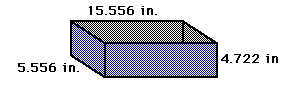

we see that one side of the box will be 25 minus two times the length
of the small square. (Let x= the length of the small square). The other
side will be 15 minus two times x, and the height will be x. Thus, the equation
for the volume of the box is y = x * (25 - 2x) * (15 - 2x).
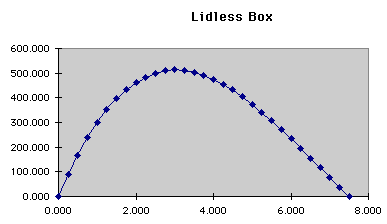
We can use the graph to find the box's maximum volume and the sizes when
the volume is 400 cubic inches.
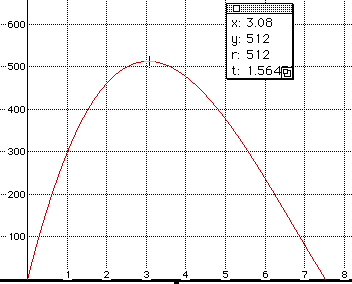
By the first graph, the maximum value appears to be 512 cubic inches, but when we zoom in on the top of the parabola,
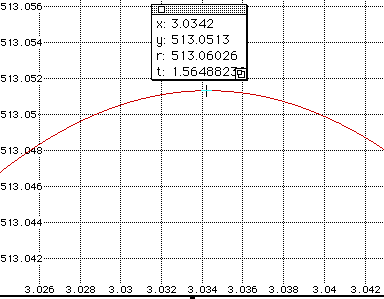
we get a better estimate, 513.0513 cubic inches. This is very close to
513.032 value that we obtained using GSP.
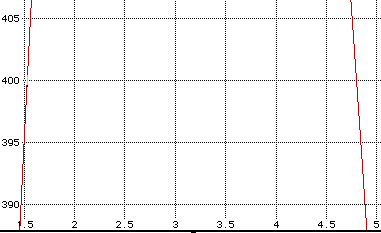
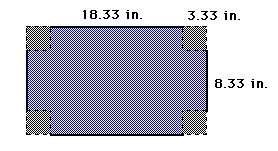
When x = 1.53, the length is 25 - 2x = 21.94 inches, and the width is
15 - 2x = 11.94 inches.
When x = 4.8, the length is 15.4 inches, and the width is 5.4 inches.
With Excel, start by placing values of x ( length of the side of the
small square) in column A. We can start with 0 and increase the values by
.25 until x = 7.5 (x can not exceed 7.5 because the width, 15 - 2x, would
be negative). In column B, we can compute the volume of the lidless box
for each of these values of x. The formula needed is A1 * (25 - 2*A1) (
15 - 2*A1). Then "fill down" column B.
The first observation is that the box reaches its maximum value when x is
between 2.75 and 3.25 inches.
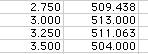
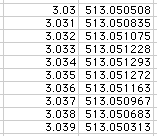
Now, start with 2.75 and increase in increments of .05, and observe that the maximum is when x is between 3 and 3.1 inches.
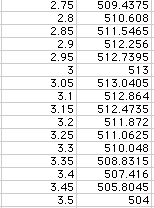
After narrowing in on the value a couple more times, we can conclude that the maximum volume of the box is 513.051293 cubic inches.
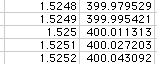
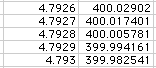
The closest values for x are 1.525 and 4.7928 inches. Thus, the lengths
21.95 and 15.4144 inches, respectively, and the widths 11.95 and 5.4144
inches.