

y = a sin (bx + c)
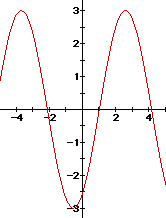
First, let b = 2 and c = 1, and let's look at the graph of
y = a sin (2x + 1) when a = 1.
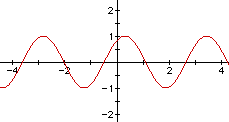
Now, overlay the graph when a = 2.
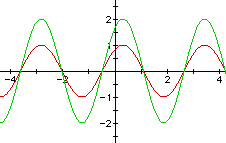
Notice that the amplitude has changed to 2.
The amplitude is still 2, but the graph is flipped.
Once again, the amplitude has been changed to a. When
a is negative, the graph is flipped. Thus, we see that
the value of a determines the amplitude and the concavity
of the graph of y = a sin (bx + c).
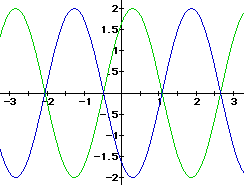
Now, overlay the graph when b = 2.
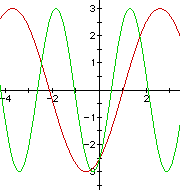
Notice that within one period of the graph when b = 1, there are two periods when b = 2.
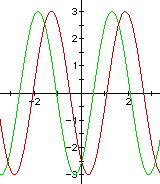
The graph still has two cycles within b = 1 (not shown), but it has been shifted to the right.
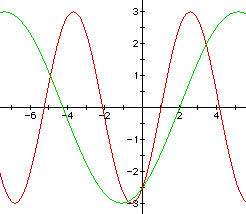
there are two periods of the graph when b = 1 contained in one period of the graph when b = 0.5. In other words, y = 3 sin (0.5 x -1) cycles one-half (0.5) time within y = 3 sin (x -1).
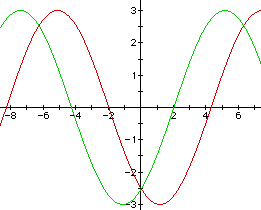
Notice that the negative value for b has again shifted the
graph to the right.
Lastly, let a = 1 and let b = 1. So,
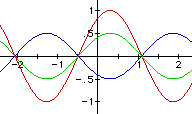
We are familiar with the graph when c = 0.
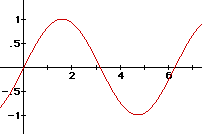
Let's see what happens when c = 1 (red), 2 (green), and 3 (blue).
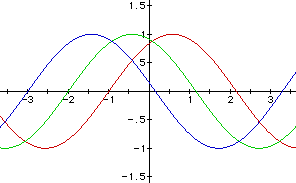
Notice that the graph shifts to the left and crosses the y-axis when y = - c.
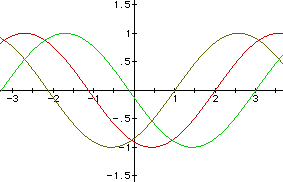
Again, the graph crosses the y-axis when y = - c.
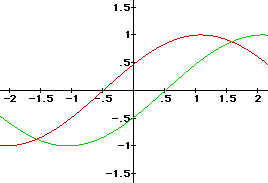
Thus, varying the value of c shifts the graph to the left and
right and the y-intercept is - c.