

First, here is a graph of
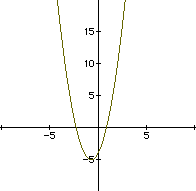
Next, we will overlay a new graph, replacing each x by (x-4).
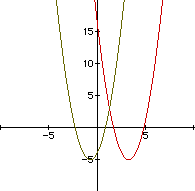
We see that this shifts the parabola 4 units to the right.
Now, we want to change the equation to move the graph into the
second quadrant. This means that the graph will need to shift
to the left; so, replace each x in the original equation by (x+4).
Also, we want to shift the graph up; so, replace y by (y-8). Thus
we have
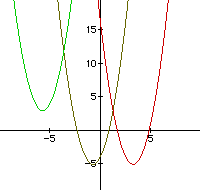
Our final objective is to change the equation to produce a
graph concave down that shares the same vertex. We know that if
we have a parabola written in standard form,![]() , then
the value of a determines rather the graph concaves
upward or downward. If a is positive, the graph
is upward. If a is negative, the graph is downward.
So, we write the equation of the parabola in the second quadrant
in standard form:
, then
the value of a determines rather the graph concaves
upward or downward. If a is positive, the graph
is upward. If a is negative, the graph is downward.
So, we write the equation of the parabola in the second quadrant
in standard form:
We see that a = 2, a positive number, which was expected since
the graph is upward. Now that the equation is in standard form,
all we need to do is change a to -2. Thus, we have a graph of
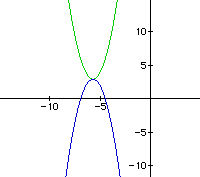
which concaves down and shares the same vertex.
Here is a slightly more convincing picture that the two graphs
share the same vertex.
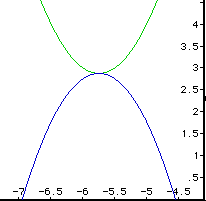
And a little more.
