

The Nine-Point circle for any triangle passes through the three mid-points of the sides, the three feet of the altitudes, and the three mid-points of the segments from the respective vertices to the orthocenter. Construct the nine points, locate the center (N) and construct the Nine-Point circle.
First, draw triangle ABC and locate the mid-point of each side.
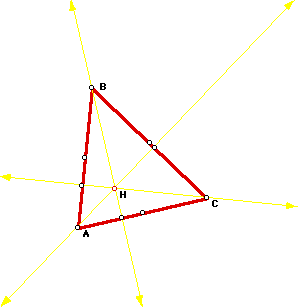
The orthocenter (H) of a triangle is the common intersection
of the three lines containing the altitudes. An altitude is a
perpendicular segment from a vertex to the line of the opposite
side.
By constructing the orthocenter of triangle ABC,
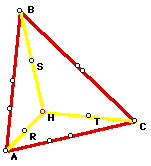
we are able to locate the next three points, the feet of the
altitudes (the point of intersection of altitude and the opposite
side). In order to construct the last three points, simply locate
the mid-points of the segments from the respective vertices to
the orthocenter.
The circumcenter of a triangle is the point in the plane
equidistant from the three vertices of the triangle. Also, it
is the center of the circumcircle of the triangle. Since
we want the Nine-Point circle to pass through all nine points
(including R, S, and T ), we can construct the circumcircle of
triangle RST.
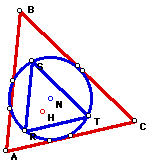
We notice that the circumcenter of triangle RST is the center
of the Nine-Point circle of triangle ABC. So, we label it N.
(Return to Write-Up
8)
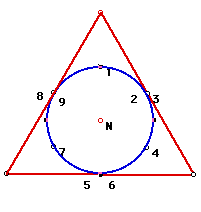
Why are some of the points the same?
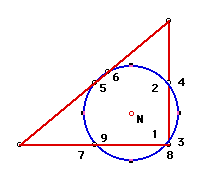
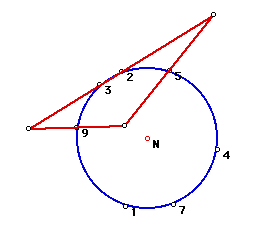
Click here to view the Nine-Point
circle of varying triangles.
Click here to see how the
center of the Nine-Point circle (N) compares to the other centers
{circumcenter (C), centroid (G), orthocenter
(H), incenter (I)} of varying traingles.
Return to Philippa's EMT Homepage