

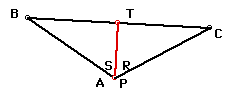
Select any triangle, ABC. If P is any point in the plane , then the three points of intersection, R, S, and T, formed by constructing perpendicular lines to the sides of ABC
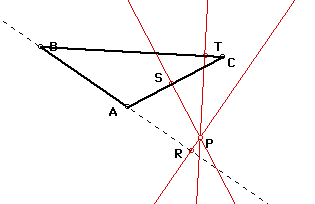
locate the vertices of the Pedal Triangle. Triangle RST is the
Pedal Triangle for Pedal Point P.
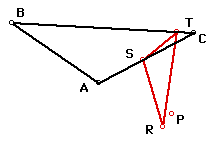
Click here (for the GSP file) to move the Pedal Point P or to change Triangle ABC.
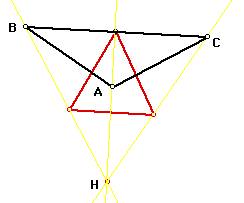
What if pedal point P is the centroid of triangle ABC?
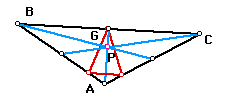
Click here to change Triangle ABC.
Click here to change Triangle ABC.
Click here to change Triangle ABC.
Click here to change Triangle ABC.
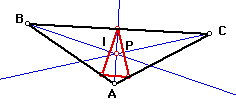
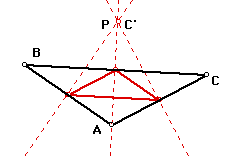
What if pedal point P is the incenter of triangle ABC?
Click here to change Triangle ABC.
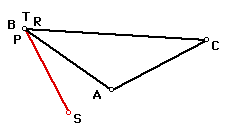
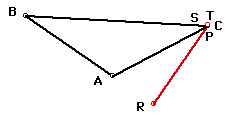
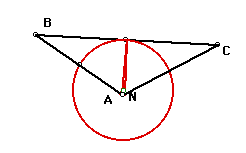
By moving the pedal point slowly to various locations so that
the three vertices of the pedal triangle remain collinear, the
path appears to be a circle. Well, it is the circumcircle of triangle
ABC.

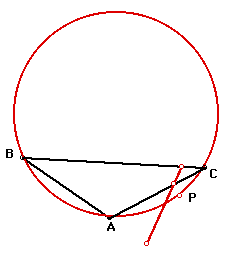
Click here for a GSP
animation of the pedal point as is moves around the circumcircle.
