
Two Tangents to a Circle
In this investigation, we will explore possible relationships between
two tangents that are drawn to a circle from a common point in the plane.
In this context, the word tangent is defined as a line, ray, or line segment
in a plane that intersects a circle at exactly one point. Here is a drawing
of a tangent segment to a circle with center A from a point D in the plane.
Point C is the point of tangency:
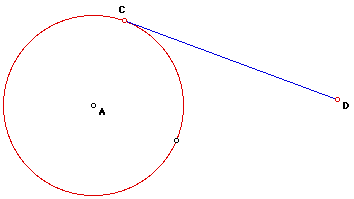
Now comes the fun part. Your job is first to construct two tangents to a
circle from a common point in the plane. Next, explore the construction
by measuring and experimenting with the different attributes of the circle
and its tangents. Come up with as many relationships/conjectures as possible.
When you are confident that you have completed this task, click here
to see a GSP file of the construction. You may click on the animate button
to see the point in the plane rotate around the circle. The file also contains
two important discoveries that you should have made.
Return to Bill Tankersley's EMT 600 Page
Return to Bill Tankersley's EMT 668 Page


