For our first class write-up, I have chosen problem 6 from assignment
1, which is to explore graphs of the type.
There is nothing earth shattering about this equation when a=1 or a=2. For
a=1, we have the line x + y = 1, which has slope -1 and y-intercept
1. For a=2, we get the circle 
, which is centered at (0,0)
and has radius 1. Since we are familiar with the shapes of these two graphs,
we will concentrate on those for a=3 and higher.
, we get the following graph: 
Quite interesting!!! We see a basic linear shape with a curved portion
near the origin in the interval [-1,1]. To further the investigation, let's
look at the graph of 
:
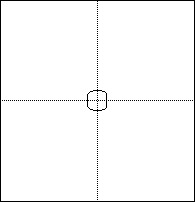
At this point in the investigation, I began to wonder if the drastic
difference in the above graphs was related to the fact that odd and even
exponents of x and y are being used in the equation. So, I graphed more
equations of this type, each time increasing the exponents. Sure enough,
I noticed that all the graphs with a being an odd
number had the same appearance as the first graph above (basically linear
with a curved portion near the origin), and all the graphs with a
being an even number had the same general appearance as the second graph
above (circular for relatively low values of a and square
shaped for higher values of a).
:
:
One thing that becomes quite apparent is that the curved portions of
the graphs are become more and more "square" in appearance.
My conjecture for 
is that the graph will look much like
a square centered around the origin. Here is the graph of the equation:
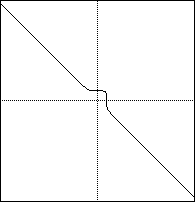
Next, my conjecture for the graph of 
is that it will
be basically linear, but with part of the square portion of the graph directly
above.
Here is the graph of :
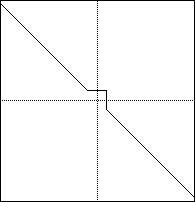
Our conjecture was absolutely correct, and this concludes the investigation
of graphs of the form .