. We will complete
this task by producing several graphs of this equation on the same axes.
We will use different values of d and make a conjecture as to the
effect of the values of d on the graphs.
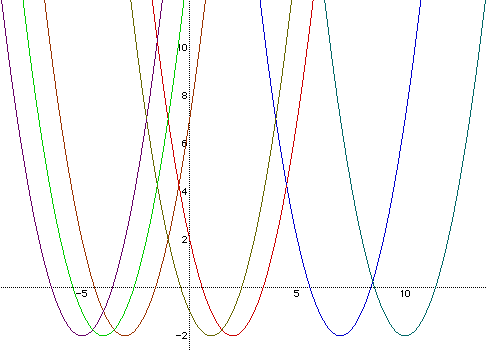
What we see from the graphs above is that varying the value of d
causes a horizontal shift in the graph of. There is no basic change
in the shape of the graph, only a change in horizontal position.
After completing the remainder of the problems from Assignment 2, there
are some conclusions to be made.
Consider the equation 
. From our investigations in this assignment,
we know that the following statements are true:
1.) The coeffecient a is a vertical stretching/shrinking factor.
For any a such that a>1, the parabola undergoes a vertical
stretch (the arms of the parabola get closer to the y axis as a gets
larger.) For any a such that a<1, the parabola undergoes
a vertical shrink (the arms of the parabola get closer to the x axis as
a gets smaller.) The coefficient a also controls the direction
(up for positive values of a and down for negative values of a)
that the parabola opens.
2.) The variable h (we used d in this investigation) is a horizontal
shifting factor. If h is positive, the parabola shifts right h
units, and if h is negative, the parabola shifts left h units.
3.) The variable k is a vertical shifting factor. If k is
positive, the parabola shifts up k units, and if k is negative,
the parabola shifts down k units. In our investigation of problem
6, we left k at a value of -2 for each graph.
This summarizes our investigations from Assignment 2.