
Bill Tankersley's EMT 668 Page
Write-up 8
Altitudes and Orthocenters
After completing each of the exercises in assignment 8, I decided to
focus on a conjecture that I made from the construction of exercises 1 through
6. Below is a list of the tasks required to complete the construction:
1. Construct any triangle ABC.
2. Construct the Orthocenter H of triangle ABC.
3. Construct the Orthocenter of triangles HBC, HAB, and HAC.
4. Construct the Circumcircles of triangles ABC, HBC, HAB, and HAC.
Here is a drawing of the finished construction:
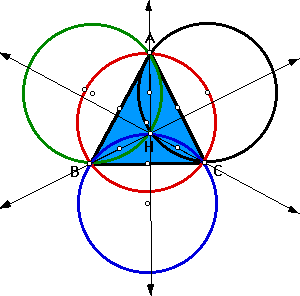
Before we get deeply involved in the conjecture I wish to make, I would
like to point out something that I found interesting. When constructing
the Orthocenters of triangles HBC, HAB, and HAC, I found the following:
Point A is the Orthocenter of triangle HBC, Point B is the Orthocenter of
triangle HAC, and Point C is the orthocenter of triangle HAB. As supporting
evidence, we determined in write-up 4 that the Orthocenter of an obtuse
triangle lies on the exterior of the triangle.
Now, after constructing the four required Circumcircles, I thought it would
be interesting to connect the centers of the Circumcircles of triangles
HBC, HAB, and HAC to form a triangle. After doing this, and creating the
corresponding polygon interior (yellow), I got the following picture:
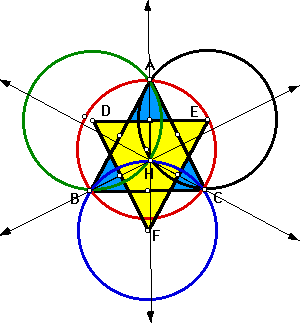
My conjecture is as follows: The area of triangle ABC (blue) is always equal
to the area of triangle DEF (yellow). My conjecture rests upon the fact
that segments BC and DE are congruent, segments CA and FD are congruent,
and segments AB and EF are congruent. Therefore, if two triangles have corresponding
sides that are congruent, the triangles themselves must be congruent. To
see a GSP sketch, click here.
From the drawing above, we can also see that the congruent segments are
translations of each other in the plane.
Another interesting thing that I noticed from the construction is this:
A line that passes through the center of one of the circumcircles of triangles
HBC, HAC, or HAB and the circumcenter of triangle ABC also passes through
the midpoint of one of the sides of triangle ABC. See the following diagram:
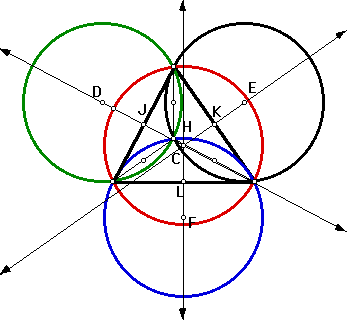
Points J, K, and L represent the midpoints of the sides of the triangle.
Notice that Points C,K,E are on the same line. The same is true for points
C,J,D, and points C, L, F.
Return to Bill Tankersley's EMT 668 Page




