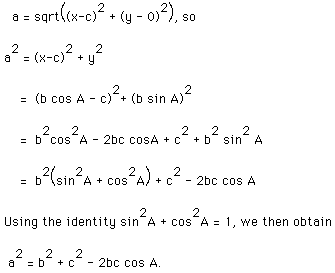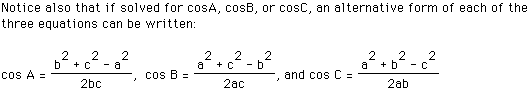Department of Mathematics Education
EMT 669, J. Wilson
An Instructional Unit
on
The Law of Sines
and
The Law of Cosines
Introduction
Having taught trigonometry in a high school setting for the past two years,
I have experience with teaching the Law of Sines and the Law of Cosines.
Although both laws are different in their appearance, they both essentially
serve similar purposes, which is finding missing angle measures and side
lengths of triangles. Technology can play an enormous role in helping students
gain a better understanding and appreciation for the proof as well as the
application of the two laws. My goal here is to present about two weeks
worth of material on the two laws, which relies on technology as the primary
method of instruction. Since we are dealing with triangles, I will specifically
focus on the use of Geometer's Sketchpad for the unit. I find that GSP works
really well for the purpose of demonstrations. For this unit, I will give
some practice problems and a quiz on the two laws separately. The two quizzes
could be merged together to form a unit test if desired. The unit could
be supplemented with additional practice problems if necessary. The solutions
to the practice problems and quizzes will be located on a separate web page
which will be linked back to this page.
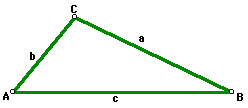
We begin our new unit by examining the following diagram:
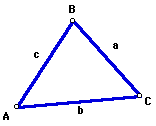
This is an example of an oblique triangle, which is a triangle with
no right angles. Although this particular oblique triangle has all acute
angles, we could just as well have an oblique triangle with an obtuse angle,
as shown below:

Recall that to "solve" a triangle means to find all three
side lengths as well as each of the angle measures. We have already learned
how to solve right triangles, so now we are going to learn how to do the
same thing with oblique triangles. Also recall that as standard notation,
we label the angles of a triangle as A, B, and C, and their opposite sides
as a, b, and c.
To solve an oblique triangle, we need to know the measure of at least one
side and any two other parts of the triangle - either two sides, two angles,
or one angle and one side. This breaks down into the following four possible
cases:
1. Two angles and any side (AAS or ASA)
2. Two sides and any angle opposite one of them (SSA)
3. Three sides (SSS)
4. Two sides and their included angle (SAS)
You may be wondering why there is no AAA in the list above. In other words,
why can we not solve an oblique triangle if the only information we know
is the measures of its three angles? The answer to this may not be obvious
until you actually look at a couple of triangles, shown below:
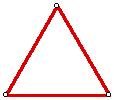

Both of these triangles have the same exact angle measures, which happen
to be 60 degrees for each angle. Therefore, simply giving three angle measures
in a triangle does not uniquely determine the side lengths of the triangle.
There are infinitely many triangles whose angles measure 60 degrees, or
any other number of degrees.
Examples
Let's look at an example problem now. Suppose we had a triangle with C=102.3
degrees, B=28.7 degrees, and b=27.4 feet, as shown below:
How could we go about finding the measure of the remaining angle and
sides? Well, if we remember that the sum of the interior angles of a triangle
is 180 degrees, then we could add up the two given angle measures and subtract
from 180, leaving us with a measure of 49 degrees for angle A. How about
the measures of sides a and c?
To help solve this triangle and many others like it, let's examine the following
diagram:
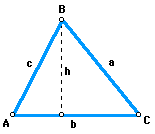
Here, we see triangle ABC and the altitude from angle B to side b, labeled
h. Let's look at a couple of trigonometric ratios involving angles in the
above triangle:
sin A = h / b
sin C = h / a
If we solve both of these equations for h, we get the following:
a * sin C = c * sin A
After manipulating this equation, we can make the following statement:
(a / sin A) = (c / sin C)
Note that neither sin A nor sin C can equal 0, since no angle of a triangle
can have a measure of 0 degrees or 180 degrees.
In a similar manner, if we constructed an altitude from vertex C to side
c, we can show the following:
(a / sin A) = (b / sin B)
Therefore, we can conclude that the following statement is true:
(a / sin A) = (b / sin B) = (c / sin C)
Likewise, the following must be true:
(sin A / a) = (sin B / b) = (sin C / c).
Both of these statements are known as the Law of Sines.
Click here to examine a sketch of the Law of
Sines. Click and drag on any vertex of triangle ABC and watch the values
change, maintaining the equalities stated by the Law of Sines.
Now, let's return to the example problem above, where we were finding
the remaining side lengths of triangle ABC. By the Law of Sines, we have:
(a / sin A) = (b / sin B)
(a / sin 49) = (27.4 / sin 28.7)
Solving for a, we find that a = 43.06 feet. Likewise, to find c, we have:
(b / sin B) = (c / sin C)
(27.4 / sin 28.7) = (c / sin 102.3)
This leads to finding that c = 55.75 feet. It is always important to
sketch the triangle and check for feasibility of the answers. Remember that
the longest side lies opposite the largest angle, and the shortest side
lies opposite the smallest angle of a triangle.
Now, let's stop and analyze the Law of Sines and come up with an understanding
of the givens we must have in order to use the Law of Sines. Since the Law
of Sines involves two angle measures and two side lengths, we know that
if we are only given the measures of three sides of a triangle, SSS, the
Law of Sines is unable to help us in this situation. Likewise, if we are
given two sides and their included angle, SAS, we will again be unable to
use the Law of Sines to solve the triangle. (Think about it for a minute!!)
Therefore, the Law of Sines only works for the following two cases, mentioned
at the beginning of the unit:
1. Two angles and any side (AAS or ASA)
2. Two sides and any angle opposite one of them (SSA)
We have already seen an example of #1 above, which was AAS. Let's look at
an example given ASA:
A pole tilts toward the sun at an 8 degree angle from the vertical, and
it casts a 22-foot shadow. The angle of elevation from the tip of the shadow
to the top of the pole is 43 degrees. How tall is the pole?
First, we need a drawing of the situation. Let's have side a represent the
pole:

Note that A = 43 degrees, and B = 90 degrees + 8 degrees = 98 degrees.
Thus, angle C = 180 - (43+98)= 39 degrees. Using the Law of Sines, we have:
(a / sin A) = (c / sin C)
(a / sin 43) = (22 / sin 39)
Thus, a = 23.84 feet.
Now, our last example of the Law of Sines involves a triangle for which
we were given two side lengths and an angle measure opposite one of the
sides. Before we start the example, let's try the following activity:
Sketch a triangle ABC such that a=12 meters, b=31 meters, and A=20.5 degrees.
After giving this activity to students, you may be surprised at the results.
Some students may draw a triangle that looks like the following:

After measuring each of the angles and side lengths, we see that this
is definitely a valid triangle. Next, some students may draw a triangle
that looks like the following:
Wait a minute!!! This is also a valid triangle for the given information.
How did this happen???? It looks like there are two distinct triangles that
can be drawn from the given information. Wow, this SSA thing looks like
a lot of trouble. (Gotta be careful how we spell SSA, too, huh?) This leads
to the following discussion.
SSA (The Ambiguous Case)
There are three possible situations that can occur when you are given two
side measures and one opposite angle measure of a triangle:
1) No such triangle exists
2) One such triangle exists
3) Two distinct triangles may satisfy the conditions. (This is the case
we just observed.)
Let's begin to make some sense out of this. Here are some criteria that
will help you determine the possibilities:
Let's refer to the angle we are given as angle A, which is either acute
or obtuse.
If A is acute, we have the following:
1) if a < h, there is no such triangle
2) if a = h or if a>h, there is one such triangle
3) if h < a < b, there are two such triangles
If A is obtuse, we have the following:
1) if a < h or if a = h, there is no such triangle
2) if a > h, there is one such triangle
Recall that in order to calculate the value of h, we use the equation h
= b sin A.
Let's look at another example of the SSA case. Suppose we are given
a triangle such that a = 10 in., b = 12 in., and A = 62 degrees. Determine
the number of possible triangles.
Let's first calculate the value of h. Since h = b sin A, we have h = 12
* sin 62 degrees = 10.6
Now, we know that A is acute and a < h. This tells us that there is no
such triangle.
Let's try one more. Suppose we are given a triangle such that A = 98
degrees, a = 10, and b = 3. Determine the number of possible triangles.
We have h = b Sin A = 10 * sin 98 degrees = 9.9
Therefore, we have that a > h and A is acute, so there is one such triangle.
Remember that it is important to sketch the triangle to make sure that the
result is feasible.
Practice Problems - Law of Sines
Use the given information to find the remaining sides and angles of the
triangle:
1. A = 30 degrees, B = 45 degrees, a = 10.
2. C = 120 degrees, B = 45 degrees, c = 20.
3. A = 36 degrees, a = 8, b = 5.
4. C = 145 degrees, b = 4, c = 14.
Click here to examine the solutions to the
above practice problems.
Quiz - The Law of Sines
Use the given information to find the remaining sides and angles of the
triangle:
1. A = 110 degrees, a = 125, b = 100
2. A = 58 degrees, a = 11.4, b = 12.8
3. A = 58 degrees, a = 4.5, b = 12.8
4. The angles of elevation to an airplane from two points A and B on level
ground are 51 degrees and 68 degrees, respectively. The points A and B
are 2.5 miles apart, and the airplane is east of both points in the same
vertical plane. Find the altitude of the plane.
5. A family is traveling due west on a road that passes a famous landmark.
At a given time, the bearing to the landmark is N 62 degrees W, and after
traveling 5 miles farther the bearing is N 38 degrees W. What is the closest
the family will come to the landmark while on the road?
Click here to examine the solutions to the
quiz.
Recall that the Law of Sines requires that either two angle measures
and one side length (ASA and AAS) be known or two side lengths and an angle
opposite one of the sides be known. This leaves the SSS and SAS cases still
unsolvable.
Consider the following diagram:

In the figure, note that point B has coordinates (c,0). Furthermore,
C has coordinates (x,y),
where x = b cos A and y = b sin A. Since a is the distance from vertex C
to vertex B, it follows from the distance formula that:
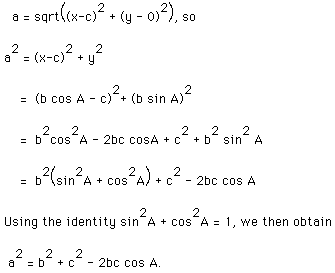
This result is known as the Law of Cosines.

Click here to examine a sketch of the Law
of Cosines. Click and drag on any vertex of triangle ABC and watch the values
change, maintaining the equalities stated by the Law of Cosines.
It is quite interesting here to note that if angle A measures 90 degrees
in the drawing above, then
cos A = 0, and we have the Pythagorean Theorem, 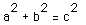 . Thus, it appears
that the Pythagorean Theorem is just a special case of the Law of Cosines.
. Thus, it appears
that the Pythagorean Theorem is just a special case of the Law of Cosines.
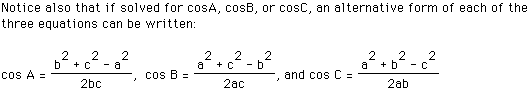
Now, we will see a couple of examples of the Law of Cosines. Remember that
we will use the Law of Cosines when we are given SSS or SAS.
Find the three angles of a triangle whose sides have lengths a = 8 feet,
b = 19 feet, and c = 14 feet.
It is wise to find the measure of the largest angle first, for this determines
the size of the remaining angles.
From the law of Cosines, we have the following:
cos B = (8*8 + 14*14 - 19*19)/ (2*8*14) = -.45089
Since cos B is negative, you know that B must be obtuse, since cosine is
negative in the second and third quadrants. Using the inverse cosine function,
we see that B = 116.8 degrees. At this point, we could use the Law of Cosines
again to find the measures of angles A and C, however it is simpler to revert
back to the Law of Sines to obtain the following:
sin A = 8 * (sin 116.8 / 19) = 0.37582. Since angle B was obtuse, A and
C must be acute.
Thus, A = 22.08 degrees and C = 180 - 22.08 - 116.8 = 41.12 degrees.
Next, let's try an example of SAS.
The pitcher's mound on a softball field is 46 feet from home plate and the
distance between the bases is 60 feet. How far is the pitcher's mound from
first base?
Let's look at a diagram for the problem:

We know that the angle formed at home plate is 45 degrees, since the
line from the pitcher's mound to home plate bisects the angle formed by
the first base line and the third base line. Using the Law of Cosines, we
get the following:
 = 46*46 + 60*60 - 2*46*60*cos 45 degrees = 1812.8
= 46*46 + 60*60 - 2*46*60*cos 45 degrees = 1812.8
Therefore, the approximate distance (d) between the pitcher's mound and
1st base is:
d = 42.58 feet.
Practice Problems - Law of Cosines
Use the given information to find the remaining sides and angles:
1. a=5, b=7, c=10
2. A = 30 degrees, b=10, c=20
3. C = 15 degrees, a=6.25, b=2.15
4. A = 120 degrees, b=3, c=10
5. Two ships leave a port at 9 a.m. One travels at a bearing of N 53 degrees
W at 12 miles per hour and the ot her at a bearing of S 67 degrees W at
16 miles per hour. Approximately how far apart are they at noon that day?
Click here to examine the solutions to the
above practice problems.
Quiz - Law of Cosines
1. A triangular parcel of land has 375 feet of frontage, and the other
boundaries have lengths of 250 feet and 300 feet. What angles does the
frontage make with the two other boundaries?
2. In order to determine the distance between two aircraft, a tracking
station continuously determines the distance to each aircraft and the angle
A between them. Determine the distance a between the planes when A = 42
degrees, b = 35 miles, and c = 20 miles.
3. Refer to the example above involving the softball diamond. On a baseball
field, the bases are 90 feet apart and the pitcher's mound is 60 feet from
home plate. a) How far is it from the pitcher's mound to third base? b)When
a runner is halfway from second to third, how far is the runner from the
pitcher's mound?
4. Use the Law of Cosines to find the missing information: a = 1.42, b
= 0.75, c = 1.25
Click here to examine the solutions to the
quiz.
Click here
for a similar web page on the Law of Sines and the Law of Cosines.
Return to Bill's EMT 669 Page