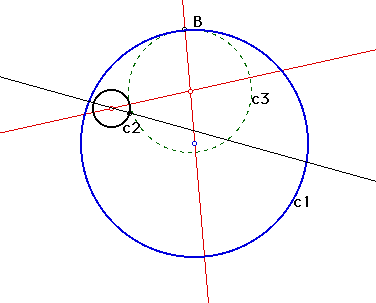

The distance from the center of circle c2 to the intersecting line (the line from the point of tangency B through the center of circle c1) can be defined as the radius of c2 plus the radius of the tangent circle.
Can we use this new knowledge? Let's take a look at our image with only the information that we know thus far. Remember, the tangent circle is only in the above image to guide us.
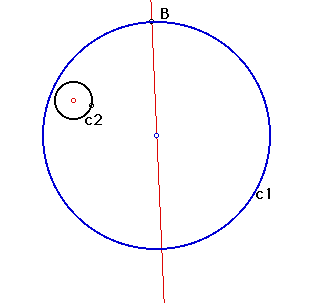
How can we use the other information we already know?
Information that we know:
The line connecting the center of the circle to the line (from point B to the center of c1) intersect.
The distance from the center of circle of c2 to the intersecting line is the radius of c2 plus the radius of the tangent circle.
The tangent circle is internal to circle c1 (it is inside) and it is tangent at point B.
Make a conjecture using this information about how we can determine the distance on the line at which it intersects the line from c2. It may help to look at the image at the bottom of the page and to see if there are any geometric figures that 1) can be constructed with our given information and 2) will help determine a length that is equal from the center of c2 to the intersection of the line.
Click Here to continue the investigation.
