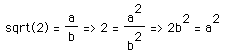
Click here for the original question.
Sqrt(2) is irrational.
Suppose that sqrt(2) is a rational number a/b where a/b is in reduced form. Then
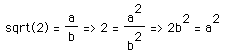
This implies that a squared is even which implies a is even. Since a is even, a = 2c for some integer c . We can substitute this into the equality above.
This implies that b is even. If a and b are even then a/b is not in lowest terms. -><- We have a contradiction. Therefore, sqrt(2) is irrational.
This type of proof will work for any N > 1 that is not a perfect square. You'll be able to see the generalization with the proof that sqrt(15) is irrational.
Sqrt(15) is irrational.
Suppose that sqrt(15) is a rational number a/b where a/b is in reduced form. Then
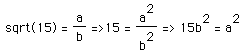
This implies that 3 dividesa squared which implies 3 dividesa . Since a is a multiple of 3, a = 3c for some integer c . We can substitute this into the equality above.
This implies that 5b squared is a multiple of 3. Since 3 does not divide 5, it must divide b squared. This implies b is a multiple of 3. If a and b are multiples of 3 then a/b is not in lowest terms. -><- We have a contradiction. Therefore, sqrt(15) is irrational.