Click here for the original question.
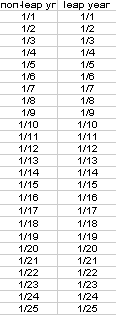
To solve this problem, I resorted to a spreadsheet. In the first two columns, I placed the number of each of the days of the year for a non-leap year and for a leap year. For example,

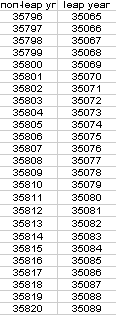
But MS Excel and other spreadsheets decode the date as a number (as seen below). It is these numbers that MS Excel uses in the calculations that follow. For us, the only important information is the difference between the dates.
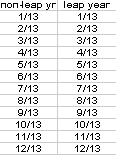
Next, I set up two columns whose cells referenced the 13th day of each month.
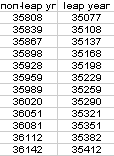
Or alternatively,
I now know when the 13th day of each month occurs. Next, I need to know how many days apart these days are. So, I set up another pair of columns by subtracting the 13th of each month from 13 Jan. This gives how far from 13 Jan every other 13th of the month is.
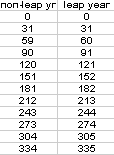
Next, I divide each of these numbers by 7 and find the remainder. The function is =MOD(cell,7). The result is as follows:
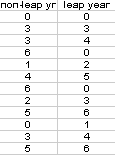
Notice that all the numbers from 0 to 6 are represented. This tells us that the 13th of the months fall on every day from Sunday (0) to Saturday (6). So, if 13 Jan falls on a Sunday, then 13 Feb and 13 Mar will occur three 'days' later, i.e., on Wednesday in a non-leap year. The 13 Apr will occur 6 'days' after 13 Jan, i.e., on a Saturday.By the manipulation of which day of the week 13 Jan upon, we can determine how many Friday 13th occur. But if we 'move' 13 Jan to Monday, then each of the values in the table above will increase by 1. Thus, we need only to count how many times each days occur from the table above to determine how many Friday 13th will happen.
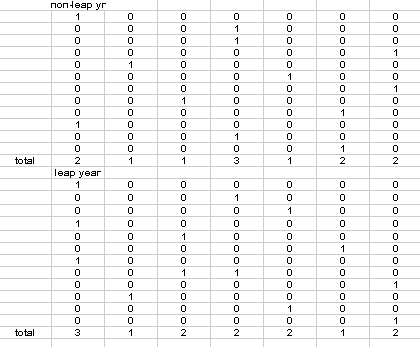
By using if-then statements, I had the spreadsheet calculate how many times the 13th of the month fall upon each day of the week (Sunday is the first column). Recall each of these days can be moved by assuming a different day of the week for 13 Jan. That is, any of the columns could be for Friday. Thus, I have shown that there is at least one Friday 13th and at most 3 Friday 13th each year.
To get a copy of the spreadsheet, click here.