Click here for the original question.
From my history of math class I recall Fibonacci's Method for writing fractions in terms of unit fractions. The first step is to find between what two consecutive integers, the inverse of the fraction occurs. That is,
Since n+1 and n are consecutive integers, and n+1 is in the numerator, the fraction (n+1)/n > 1. Since n+1 is not twice n (except for n=1), the fraction (n+1)/n < 2. The inverse of he above relation is,
The next step is to find the difference between the given fraction and the lower bound above.
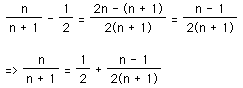
We now have the fraction in terms of one unit fraction and another fraction. In order to make the second a unit fraction, n must equal 2. If n=1, we only have one unit fraction which will not be a solution. If n>1, then the second fraction can be split into 2 or more unit fractions. Thus the only fraction that can be decomposed into only two unit fractions is
While checking my answer, I decided to try a different method to see if I could get another decomposition. That is, I added the two 'simplest' fractions, 1/2 to 1/3, and found the following:
So, 5/6 can be expressed in terms of two unit fractions. I continued by trying a few more of these and found the following:
At this point, I set up a spreadsheet to test the sums of various pairs of unit fractions. As the integers increased in the unit fractions, the sums decrease. But as n increases, the fraction
tends towards 0. That is,
the lim as n -> infinity of ![]() =
=
the lim as n -> infinity of ![]() = 0.
= 0.
I initially set up my spreadsheet to include 1/2 to 1/25, but quickly realized that I did not need to find all this data. I already had the 4 possible fractions of the form n/(n+1) that can be expressed and the sum of two different unit fractions.