Click here for my copies of the questions. Click here for the original page of questions.
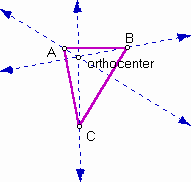
1. Construction of the orthocenter: Given the triangle ABC For each side construct a perpendicular line to the side that passes through the opposite vertex.

The intersection of these lines is the orthocenter of the triangle. It is possible that the orthocenter is outside the triangle.
2: Descriptions of orthocenter and some theorems and conjectures:
CONJECTURE: The orthocenter is outside the triangle when the triangle has an obtuse angle.
CONJECTURE: For a right triangle, the orthocenter occurs at the vertex that contains the right angle.
CONJECTURE: The points F, G, H lie on the nine-point circle. click here for the GSP file.
THEOREM: The orthocenter, centroid and circumcenter are collinear. That is they all lie on the Euler line.
CONJECTURE: Also, if another triangle is constructed using the points F, G, H (seen in the above figure), then the orthocenter of triangle ABC coincides with the orthocenter of triangle FGH when the triangle ABC is equilateral. Click here for the GSP file.
CONJECTURE: If ABC is an equilateral triangle, then the circumcenter of triangle FGH (where F,G,H are constructed as shown in the above figure) coincides with the orthocenter of triangle ABC. Click here for GSP file.
THEOREM (Ceva): Given any point inside a triangle, for each vertex construct the line that passes through the vertex and the given point. Construct the intersection of these lines with the sides of the triangle. (See the figure above.) Then (CH)(BG)(AF)/(HB)(GA)(FC)= 1.
CONJECTURE: April's center is the incenter.
Back to previous page