1.
I. Area of a triangle is 1/2 ab sin(C).
(a) A GSP sketch that checks this
law.
(b) See GSP sketch.
(c) A surveyor is contracted to measure the area of a triangular
piece of land. She is standing at one 'vertex' of the plot of
land. She has measured the lengths of the two sides which end
where she is standing. They measure 14 km and 22 km. She knows
the angle between the two lines is 48 degrees. What is the area
of the plot of land?
II. Law of cosines: c^2 = a^2 + b^2 - 2ab cos(C).
(a) A GSP sketch that checks this
law.
(b) See GSP sketch.
(c) Eli Cooley flew his plane 900 km north before turning his
plane 15 degrees clockwise. He flew 1150 km in this new direction
and then landed his plane. How far is Eli from his starting point?
Source: Burrill, G. F. (1995). Geometry: Applications and
Connections. Macmillan/McGraw-Hill Publishing Co.
III. Law of sines: a/sin(A) = b/sin(B) = c/sin(C).
(a) A GSP sketch that checks this
law.
(b) See GSP sketch.
(c) The support for a powerline that stands on top of a hill is
60 ft tall. A surveyor stands at a point on the hill and observes
that the angle of elevation to the top of the support measures
42 degrees and to the base of the support measures 18 degrees.
How far is the surveyor from the base of the support? Source:
Burrill, G. F. (1995). Geometry: Applications and Connections.
Macmillan/McGraw-Hill Publishing Co.
III. Addition formulas: sin(a + b) = sin a cos b + cos a sin b AND cos(a + b) = cos a cos b - sin a sin b.
(a) DNF.
(b) DNF.
(c) DNF.
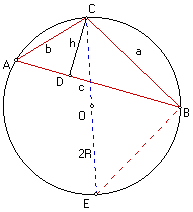
2. Prove that for a triangle ABC with circumradius R, the area of ABC is equal to abc/4R.

Given triangle ABC. Construct the altitude CD. Then, the area of ABC = 1/2 hc by definition. Construct the circumcircle of the triangle ABC. Construct the diameter CE. So, d(CE) = 2R where R is the circumradius. Construct the line segment BE. (CBE) =1/2 m(COE) = 1/2 (180 degrees) = 90 degrees. m(CAB) = m(BEC) because tey subtend the same arc. m(CAD) = m(CAD) by angle measure theorem. So triangle CAD is similar to triangle BEC by AA theorem. So, by definition of similarity, 2R/b = a/h. This implies ab/2R = h. Multiplying both sides by 1/2 c we get abc/4R = 1/2 hc. Thus, abc/4R = area(ABC) by transitivity. QED
3. Let ABC be a triangle with circumradius R. Suppose that c1 and c2 are circles such that both c1 and c2 pass through the point A, c1 is tangent to BC at B, and c2 is tangent to BC at C. Let p be the radius of c1 and q be the radius of c2. Prove that pq = R^2.
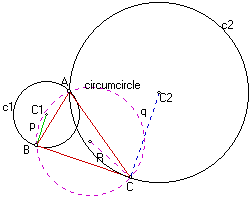
Given triangle ABC constructed as stated above. Construct a circle with center C and radius R. Construct the intersection, S, of the circle with line segment BC. Construct a line through CC2. Construct a circle with center C and radius q. Construct the intersection, T, of the circle with the line CC2.
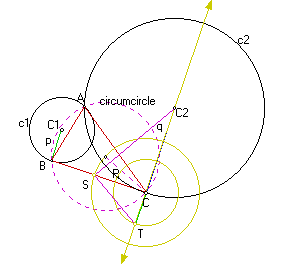
We now have triangle STC2 where d(TC2) = p + q, the altitude, SC has length R, d(TC) = p and d(CC2) = q. See note below.
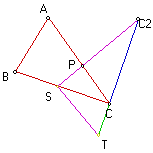
Construct the line through points S and C2. Construct the perpendicular line to line segment TC2 through point T. Construct the intersection, Y, of these two lines.
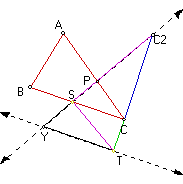
Let m(YC2T) = beta and m(STY) = alpha. So, m(TYC2) = 90 - beta and m(CSC2) = 90 - beta by the traingle angle sum theorem. Since m(C2CS) = 90 degrees, then m(CSC2) + m(YC2T) = 90 degrees. So, m(TSC2) = 90 degrees. Thus, by gemonteric mean, we have R^2 = pq.
Note: From the noted point above, there is a better proof on a GSP sketch. This newer version of the proof's end was posted on the website at 1:55 pm Thursday whereas all the other work was posted prior to class.
4. Prove that for a triangle, if D is the midpoint of side AB, then the length m of the median CD satisfies the equation m^2 = 1/2 a^2 + 1/2 b^2 - 1/4 c^2.
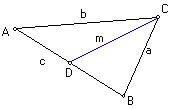
Given triangle ABC. Construct median CD where D is the midpoint of AB. By the law of cosines b^2 = (1/2 c)^2 + m^2 - 2(1/2 c)m cos(CDA) and a^2 = (1/2 c)^2 + m^2 - 2(1/2 c)m cos (BDC). Adding these two we get a^2 + b^2 = 1/2 c^2 + 2 m^2 (where cos (CDA) = -cos(BDC)*). Rearranging, we get m^2 = 1/2 a^2 + 1/2 b^2 - 1/4 c^2. QED
*NOTE: For supplementary angles a and b, cos(a) = cos(180 - b) = cos(180) cos b + sin(180) sin b [note also that cos(-b) = cos(b) and sin(-b) = -sin(b)] by angle addition formula for cos. Since cos(180) = -1 and sin(180) = 0, we have cos(a) = cos(180 - b) = -cos b.
5. (XC) Prove ac + bd = mn for a cyclic quadrilateral.
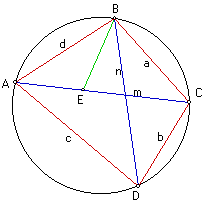
Given cyclic quadrilateral ABCD. Construct line segment BE such that m(ABE) = m(DBC). m(CAB) = m(CDB) since these angles subtend the same arc. So, triangle ABE is similar to triangle DBC by AA theorem. So, d = kn and d(AE) = kb by the definition of similarity. So, d/n = d(AE)/b [or db = nd(AE)] by transitivity. m(ABD) = m(ABE) + m(EBD) [by angle measure theorem] = m(DBC) + m(EBD) [by substitution] = m(EBC) [by angle measure theorem]. m(BDA) = m(BCA) since these angles subtend the same arc. m(BCA) = m(BCE) by angle measure theorem. So, m(BDA) = m(BCE) by transitivity. Thus, triangle ABD is similar to triangle EBD by AA theorem. So, c = k'd(EC) and n = k'a by the definition of similarity. So, c/d(EC) = n/a [or ac = nd(EC)] by transitivity. So, adding db = nd(AE) and ac = nd(EC), we obtain ac + bd = nd(AE) + nd(EC) = n(d(AE) + d(EC)) [by distributive property] = nm [by distance theorem]. Therefore, ac + bd = mn. QED
contact me
return to main geometry page