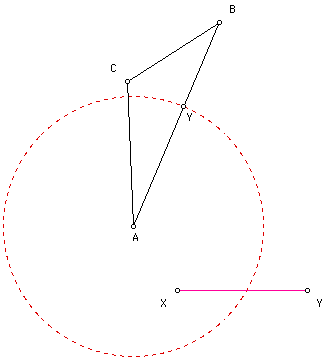
6. Given triangle ABC and segment XY, construct a point Z so that the triangle XYZ is similar to triangle ABC.
Click here for a GSP sketch of the construction.
Click here for a JSP sketch of the construction. NOTE: you will need a java-enabled browser.
Construction:
Given triangle ABC and segment XY. Construct a circle with center A and radius of length = d(XY). Construct the intersection (point Y) of the circle with the line passing through points A and B. Let point X correspond to point A.

Construct through point Y a line parallel to side BC. Construct the intersection (point Z) of the parallel line and the line that passes through the points A and C. Construct the segments YZ and ZX
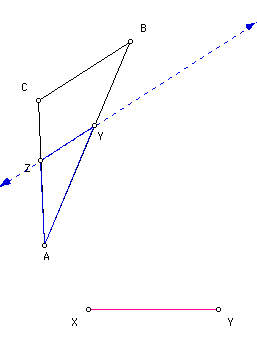
Triangle XYZ is similar to triangle ABC.
Proof: Angle CAB is congruent to angle ZXY (where X and A are concurrent) by angle measure theorem. Angle ZYX is congruent to angle CBA by the transversal theorem. Thus, triangle XYZ is similar to triangle ABC by AA theorem.