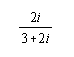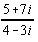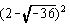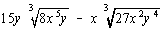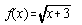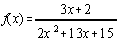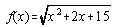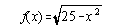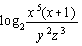Section 1
Perform the indicated operation(s) and simplify. Rationalize denominators when necessary, and write all complex numbers in the form (a + bi).
  1. (7 + 3i) + (–3 + 9i)
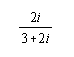
  2. section 1 - question 2

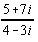
  3. section 1 - question 3

  4. i 287

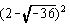
  5. section 1 - question 5

  6. section 1 - question 6

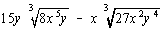
  7. section 1 - question 7

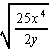
  8. section 1 - question 8

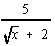
  9. section 1 - question 9

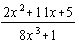
  10. section 1 - question 10

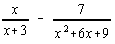
  11. section 1 - question 11

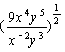
  12. section 1 - question 12

Section 2
Solve the following for x:
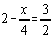
  1. section 2 - question 1

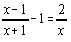
  2. section 2 - question 2

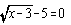
  3. section 2 - question 3

  4. 25x2 + 10x = –3

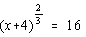
  5. section 2 - question 5

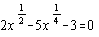
  6. section 2 - question 6

  7. 5x2 – 14x – 3 = 0

  8. x2 + 7x – 30 > 0

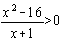
  9. section 2 - question 9

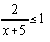
  10. section 2 - question 10

  11. | x + 4 |  > 3

  12. | x + 3 | – 2 = 4

  13. | 3x – 7 | < –2

  14. | x – 5 |  > –7

  15. How many pounds of hazelnuts which sell for $2.40 per pound should be mixed with 6 pounds of almonds which sell for $2.00 per pound to obtain a mixture which sells for $2.25 per pound.

  16. A mason can build a wall in 9 hours. An apprentice can do it in 12 hours. How long would it take them working together?

  17. Find two numbers which have a sum of 35 and a product of 174.

  18. The length of a rectangle is 4 less than twice its width. If the diagonal of the rectangle is 10 inches long, find the length and the width.

  19. The perimeter of a rectangular area is 80 cm.  If w is the length of one side, find the maximum area that can be enclosed.

  20. Find the amount to which $5000 will grow, if it is invested at an annual interest rate of 3.5% for 3 years compounded:
    (a) annually, (b) monthly, ( c) daily, (d) hourly, (e) continuously.

  21. How long will it take $2000 dollars to double if it is invested at 4% compounded continuously?

  22. How much pure gold must be added to 8 grams of a 30% alloy to get a 50% alloy?

  23. A family buys a new house for $80,000.  It is estimated that after 5 years the value of the house will be $100,000.  Find the linear function demonstrating this relationship and use that to determine the value of the house after 3 years.

  24. One positve integer is 5 less than another.  The difference of their squares is 85. Find the two integers.

Section 3
  1. Find the equation of the line through the point (–3,2) and perpendicular to the line 2y – 4x = 8. Write your solution in slope-intercept form.

  2. Find the equation of the line with y-intercept 6 and parallel to the line 3y – 5x = 7.

  3. Find the distance between the points P1 = (–4, 11) and P2 = (–7, 15).

  4. Find the distance between the points P1 = (7, 4) and P2 = (12, –1).

  5. Find the midpoint between the points P1 = (–8, 1) and P2 = (–4, 15).

  6. Find the standard form of the equation of a circle that has center C(–16,31) and radius 5.

  7. Find the center and the radius of the circle: x2 – 16x + y2 + 10y + 40 = 0

  8. Graph f(x) = –(x – 3)2 + 7 using graphing techniques.

  9. Graph f(x) = (x + 6)3  – 2 using graphing techniques.

  10. Graph f(x) = sqrt {–x} + 7 using graphing techniques.

  11. Graph f(x) = –3|x – 4|  using graphing techniques.

  12. Determine whether each of the following equations has symmetry with respect to either the x-axis or the y-axis.
    • x = | y | + 3

    • y = x2 – 7

    • y = x3 + 2x – 1

Section 4
For #1–3, find the inverse of each of the following functions and check your answers. Also, state the domain and range of both f and f inverse.
  1. f(x) = x3 – 4

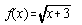
  2. section 4 - question 2

  3. f(x) = 5x – 7

For #4–8, find the domain of the following functions:
  1. f(x) = 3x/(2x – 8)

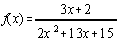
  2. section 4 - question 5

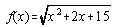
  3. section 4 - question 6

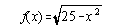
  4. section 4 - question 7

  5. f(x) = x3 – 8

Section 5
For #1–5, solve for x:
  1. 4x + 2 = 37

  2. log x + log (x + 3) = 1

  3. e2x = 8

  4. eln(x + 2) = 15

  5. log2 x + log2 (x – 1) = 1

For #6–7, write the following expression as a single logarithm:
  1. 3 log3 x + 4 log3 y – 5 log3 z

  2. 5 log x – 3 log (x + 3)

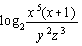
  1. Write the following expression as a sum and difference of logarithms: section 5 - question 8

  2. Sketch the graph of f(x) = 2x – 2 + 3. State the domain and range of f(x).

  3. Sketch the graph of f(x) = ln (–x). State the domain and range of f(x).

Section 6
For #1–3, use synthetic division to find the quotient and remainder when f(x) is divided by g(x).
  1. f(x) = 5x4 + 6x3 – 9x2 + 3x + 4 ;  g(x) = x + 2

  2. f(x) = x5 – 10x4 + 20x3  – 31x2  – 65 ;  g(x) = x – 8

  3. f(x) = 2x3 – 5x2 + x; g(x) = x – 2

  1. Use synthetic division to determine if g(x) is a factor of f(x): f(x) = x5 – 32 ;  g(x) = x – 2

  2. Use the remainder theorem to determine f(–5): f(x)  =  3x3 – x  + 5 

  3. Find the zeros of f(x) = (x + 5)(x2 – 25) (x + 3) 5and state the multiplicity of each.

  4. Use the rational zero theorem to list all possible rational zeros of  f(x) = 5x4 – 3x2 + 2x + 4