| Section 1 |
| 1. 4 + 12i |
2. 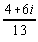 |
3. 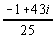 |
| 4. i3 = –i |
5. –32 – 24i |
6. 32 |
7. 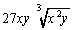 |
8. 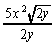 |
9. 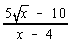 |
10. 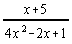 |
11. 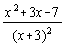 |
12. 3x3y |
Section 2 |
| 1. x = 2 |
2. x = –1/2 |
3. x = 28 |
| 4. –1/5 ± (i/5)Ö2 |
5. x = –68, 60 |
6. x = 81 |
| 7. x = –1/5, 3 |
8. (–¥, –10] È [3,¥) |
9. (–4, –1) È (4,¥) |
| 10. (–¥, –5) È [–3, ¥) |
11. (–¥, –7) È (–1, ¥) |
12. x = –9, 3 |
| 13. no solution |
14. (–¥, ¥) |
15. 10 lbs. of hazelnuts |
| 16. 36/7 hours |
17. 29 and 6 |
18. l = 6 and w = 8 |
19. The maximum area is
400 cm2 |
20. - $5543.59
- $5552.70
- $5553.53
- $5553.55
- $5553.55
|
21. approx. 17 years |
| 22. 3.2 grams of gold |
23. y = 4000x + 80000 |
24. 11 and 6 |
Section 3 |
| 1. y = –x/2 + 1/2 |
2. y = (5/3)x + 6 |
3. 5 |
4. 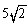 |
5. (–6, 8) |
6. (x + 16)2 + (y – 31)2 = 25 |
7. center is (8, –5)
and radius is 7 |
8. 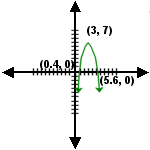 |
9. 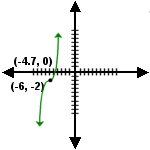 |
10. 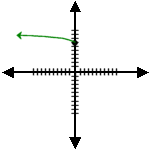 |
11. 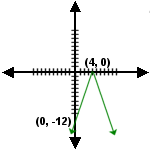 |
12.
- x = |y| + 3; symmetric about the x-axis
- y = x2 – 7; symmetric about the y-axis
- y = x3 + 2x – 1; not symmetric
|
Section 4 |
1. 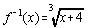
The domain and range of both f(x) and f -1(x)
is (–¥,¥). |
2. f -1(x) = x2 – 3.
The
domain of f(x) is [–3, ¥), its range is [0, ¥).
The domain of f -1(x) is [0, ¥) and its range is
[–3, ¥) |
3. f -1(x) = (x + 7)/5.
The domain and range of both f(x) and f -1(x)
is (–¥,¥). |
4. The domain of f(x) is
(–¥, 4) È (4,¥). |
5. The domain of f(x) is
(–¥, –5) È (–5, –3/2)
È (–3/2, ¥). |
6. The domain of f(x) is
(–¥, ¥). |
7. The domain of f(x) is
[–5, 5]. |
8. The domain of f(x) is
(–¥, ¥). |
|
Section 5 |
| 1. x = (log 37)/(log 4) – 2 |
2. x = 2 |
3. x = (ln 8)/2 |
4. x = 13
|
5. x = 2
|
6. 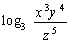
|
7. 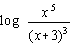 |
8. 5 log2 x + log2 (x + 1)
– 2 log2 y – 3 log2 z |
9. Domain (–¥,¥) and Range (3,¥)
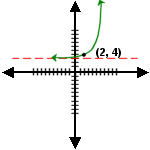 |
10. Domain (–¥,0) and Range (–¥,¥)
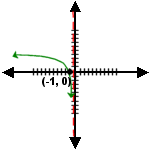 |
|
|
Section 6 |
| 1. 5x3 – 4x2 – x + 5 ; R: –6 |
2. x4 – 2x3 + 4x2 + x + 8;
R: –1 |
3. 2x2 – x –1; R: –2 |
| 4. Yes, x – 2 is a factor. |
5. f(–5) = –365 |
6. –5 multiplicity 2;
5 mulitplicity 1;
and –3 mulitplicity 5 |
| 7. ±1, ±2, ±4, ±1/5, ±2/5, ±4/5 |
|
|





