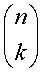 . This is calculated by:
. This is calculated by:
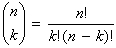 , where n! = n·(n–1)·(n–2)····2·1
and 0! = 1.
, where n! = n·(n–1)·(n–2)····2·1
and 0! = 1.The distribution of the number of successes, X in a binomial setting is called a binomial distribution with parameters n and p. The possible values of X are whole numbers from 0 to n.
Binomial coefficient: the number of ways to select k objects from n total objects. This is
represented by 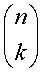 . This is calculated by:
. This is calculated by:
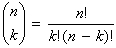 , where n! = n·(n–1)·(n–2)····2·1
and 0! = 1.
, where n! = n·(n–1)·(n–2)····2·1
and 0! = 1.
Luckily, we can perform this calculation on the TI-83 calculator!
Binomial coefficient: If X has the binomial distribution with n observations each with
probability, p, of success, then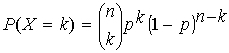
Again, we can perform this calculation on the TI-83 calculator!
If X has the binomial distribution with n observations each with
probability, p, of success, then
μ = np
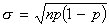
For large n and for p near 0.5, the binomial distribution can be approximated by a normal distribution. More specifically, we can use the normal approximation the the binomial distribution if the following conditions are met:
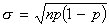 .
.