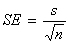.In the previous chapter we assumed that we knew σ of the population. This is not realistic. But σ is important because it affects hypothesis testing and CI! Here are the assumptions of the z–test:
.
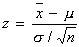What if σ is unknown? Then we estimate σ with the standard error (SE) of the sample
mean: .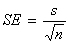
assumptions of the t distributions:
,
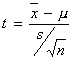where s is the sample standard deviation.
There is a different t distribution for each sample size. So, to identify the t distribution we use the degrees of freedom (df). The df for a t distribution is n – 1. We represent the t distribution as t(n – 1).
The density curve of t(k) is given by: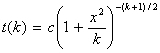 
,
where c is a constant, k is df. The t distribution looks like the standard normal, N(0, 1), curve
except that the t distribution is wider. As k increases, the t(k) curve approaches the
N(0, 1) curve. To find critical values for the t distribution see Table C of your text.
NOTE: the one–sample t–statistic procedures are analogous to the procedures for the one–sample z–statistic!
A level C CI for μ is x-bar ± t*×SE. This interval is exact when the population distribution is normal, and is approximately correct for large n in other cases. Luckily, the TI83 can calculate the t CI!
t–test for a population mean:
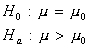
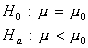
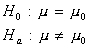
Recall: H0 and Ha always refer to the population and NOT to a particular outcome. It is often easier (and more appropriate) to state H0 and Ha before looking at the data.
Matched pairs is an experimental design that collects before-and-after observations on the same subjects. Apply the one–sample t procedures to the observed differences. Luckily, the TI83 can perform matched pairs t procedures!
A statistical inference procedure is called robust if the probability calculations do not change very much when the assumptions of the procedure are violated.