 ,
(i.e., of the sample(s)) to estimate p.
,
(i.e., of the sample(s)) to estimate p.
This chapter presents the z procedures for one–sample and two–sample inference about
population proportions, p. p is the proportion of the population that has some desired property (i.e., success).
The population proportions, p, are unknown, so we use the statistic,  ,
(i.e., of the sample(s)) to estimate p.
,
(i.e., of the sample(s)) to estimate p.

If  is the sample proportion of successes of an SRS of size n from a
large population, then
is the sample proportion of successes of an SRS of size n from a
large population, then
 is approximately normal for large n
is approximately normal for large n is an unbaised
estimator of p)
is an unbaised
estimator of p)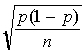
 is a more accurate
estimator of p when n is large.
is a more accurate
estimator of p when n is large.
The z statistic is 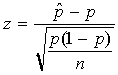 .
.
The distribution of the z statistic is approximately standard normal, N(0, 1) when:
 is NOT valid when
there are too few or too many successes in the sample.
is NOT valid when
there are too few or too many successes in the sample.
Since p is NOT known, we need to use the standard error as an estimate of the s.d.:
SE = 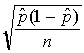 . This is valid because for large n,
. This is valid because for large n,  is close to p.
is close to p.
A level C CI for p is  ± z*×SE.
Luckily, the TI83 can calculate the one–sample proportion z CI!
± z*×SE.
Luckily, the TI83 can calculate the one–sample proportion z CI!
The one–sample z–test for a population proportion:
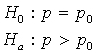
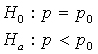
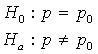
Recall: H0 and Ha always refer to the population and NOT to a particular outcome. It is often easier (and more appropriate) to state H0 and Ha before looking at the data.
NOTE: Here is a great quote from the text: "statistics in practice involves much more than recipes for inference" (p. 436).The margin of error is 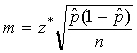 . Reaaranging, we get
. Reaaranging, we get
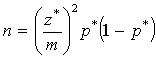
where z* is determined from N(0, 1) and p* is either a guess about p OR
p* = 0.5. The latter case is called conservative since it results in the largest sample size for a given
z* and m.