www.john-weber.com
Chapter 9: Inference for Two–Way Tables
Section 9.2: The Chi–Square Test
This test uses the observed counts and expected counts. The chi–square statistic is:
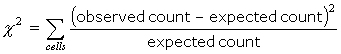 .
.
The fraction part of the statistic is calculated for
each cell of a table. Then these fraction parts are added together to form the chi–square statistic. This
is a measure of how far the observed counts are from the expected counts. As the distance between theses counts
increases, the chi–square statistic increases.
Large values of χ2 are evidence against H0.
The χ2 statistic is easy to find on the TI83 calculator.
The chi–square distributions
The chi–square distributions are a family of right–skewed distributions that take on only positive
values. A specific chi–square distribution is described by its degrees of freedom: d.f. = (r – 1)(c – 1).
The mean of the chi–square distribution is equal to d.f.!
The P–value is the area to the right of χ2 under the chi–square
density function.
More uses of the chi–square test
The chi–square test can be used to compare:
- two or more populations
- two or more independent SRSs from same population
- individuals in a single SRS whom are classified according to both of the categorical variables
The chi–square test:
- State the hypotheses for the "many–tailed test":
- H0: p1 = p2 = p3 =
··· = pn
Ha: not all of p1, p2, p3,
..., pn are equal
- Calculate the P–value
- Make your conclusion
Cell counts required for the chi–square test
The following are required in order to use the chi–square test:
- no more than 20% of expected counts are less than 5
- all individual expected counts are at least 1
- all four counts in a 2 × 2 table are at least 5
The chi–square test and the z test
We can make any r × c table into a r × 2 table by making two columns labeled,
successes and failures. Then, if r = 2 (i.e., a 2 × 2 table), there are two options to do this comparison:
- chi–square test with d.f. = 1
- two–sample proportion z test
The P–values from both tests will be equal! In this case, it is recommended to use the z test because:
- the z test permits a one–tailed test
- the z test is related to the CI for p1 – p2
Back to John Weber's MATH 1431 Page
Back to john-weber.com
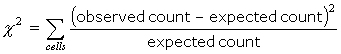 .
.