
By default mean = 0 and standard deviation = 1.
| Steps | Key Sequence | Screens |
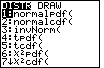
| 1. Find the inverse normal curve function | Press 2nd then VARS |  |
| Press 3 (for invNorm) |  |
|
| ** This function has three (3) arguments. They are: area, mean, standard deviation. ** | ||
| ** Area MUST be between 0 and 1. | ||
| Example 1: Let mean = 35 and standard deviation = 2 | ||
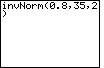
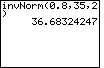
| Case 1: Find the number x such that the proportion of observations that are less than x in a normal distribution is 0.8. In other words, the area to the left of x is 0.8. | invNorm(0.8,35,2) |  |
| ENTER |  |
|
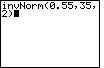
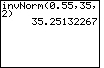
| Case 2: Find the number x such that 45% of all observations from a normal distribution are greater than x. In other words, the area to the right of x is 0.45 and the area to the left is 0.55. | invNorm(0.55,35,2) |  |
| ENTER |  |
|
| Example 2: Standard Normal Curve where mean = 0 and standard deviation = 1 | ||
| ** The standard normal curve uses z, where z = (x – mean)/(standard deviation). | ||
| ** Rearranging for x: x = mean + z * standard deviation. | ||
| ** For the standard normal curve, the invNorm function will use ONLY one (1) argument,
area. By default mean = 0 and standard deviation = 1. |
||
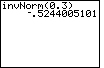
| Case 1: Find the number z such that the area under a normal distribution is 0.3 to the left of z. | invNorm(0.3) |  |
| ENTER |  |
|
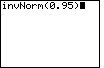
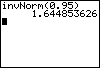
| Case 2: Find the number z such that 5% of all observations from a normal distribution are greater than z. In other words, the area to the right of x is 0.05 and the area to the left is 0.95. | invNorm(0.95) |  |
| ENTER |  |
|