Maximization of a lidless box
We are given a rectangular sheet of cardboard 15 in. by 25 in. If a small
square of same size is cut from each corner and each side folded up along
the cuts to form a lidless box. We know that the volume of the box will
be v=(base)(width)(height).
What will vary for this box will be the height so we will let x equal the
height. Therefore the equation of our box made form a sheet of cardboard
15 in. by 25 in. will be
v=(15-2x)(25-2x)(x)
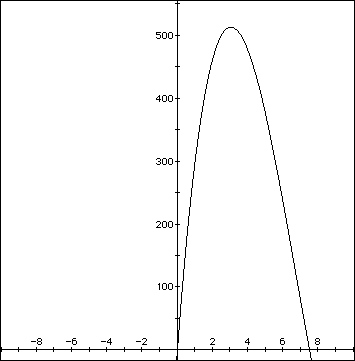
If we graph this on Algebra Xpressor we will be able to tell the maximum
volume.

We can tell from this graph that the maximum volume, of about 310, will
be achieved when x is approximately 3.
Now lets consider what this actually looks like with GSP
click here for GSP sketch
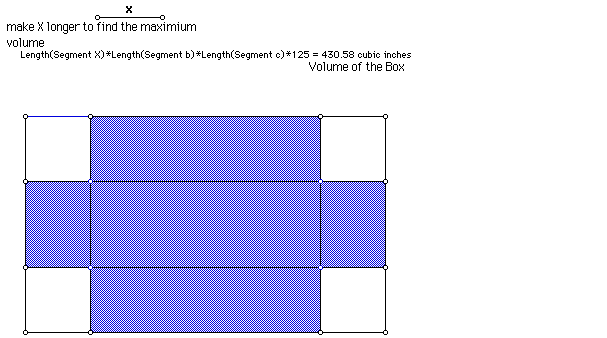
With GSP, we are able to get a more visual idea of what the cut out piece
of the card board would look like. We get the same answer of the maximum
volume being about 510 cubic inches.
Now lets get a little more exact. We will create a spreadsheet using Excel
and see how some decimal places.
height base width height volume
0.1 24.8 14.8 0.1 36.704
0.2 24.6 14.6 0.2 71.832
0.3 24.4 14.4 0.3 105.408
0.4 24.2 14.2 0.4 137.456
0.5 24 14 0.5 168
0.6 23.8 13.8 0.6 197.064
0.7 23.6 13.6 0.7 224.672
0.8 23.4 13.4 0.8 250.848
0.9 23.2 13.2 0.9 275.616
1 23 13 1 299
1.1 22.8 12.8 1.1 321.024
1.2 22.6 12.6 1.2 341.712
1.3 22.4 12.4 1.3 361.088
1.4 22.2 12.2 1.4 379.176
1.5 22 12 1.5 396
1.6 21.8 11.8 1.6 411.584
1.7 21.6 11.6 1.7 425.952
1.8 21.4 11.4 1.8 439.128
1.9 21.2 11.2 1.9 451.136
2 21 11 2 462
2.1 20.8 10.8 2.1 471.744
2.2 20.6 10.6 2.2 480.392
2.3 20.4 10.4 2.3 487.968
2.4 20.2 10.2 2.4 494.496
2.5 20 10 2.5 500
2.6 19.8 9.8 2.6 504.504
2.7 19.6 9.6 2.7 508.032
2.8 19.4 9.4 2.8 510.608
2.9 19.2 9.2 2.9 512.256
3 19 9 3 513
3.1 18.8 8.8 3.1 512.864
3.2 18.6 8.6 3.2 511.872
3.3 18.4 8.4 3.3 510.048
3.4 18.2 8.2 3.4 507.416
3.5 18 8 3.5 504
3.6 17.8 7.8 3.6 499.824
3.7 17.6 7.6 3.7 494.912
3.8 17.4 7.4 3.8 489.288
3.9 17.2 7.2 3.9 482.976
4 17 7 4 476
4.1 16.8 6.8 4.1 468.384
4.2 16.6 6.6 4.2 460.152
4.3 16.4 6.4 4.3 451.328
4.4 16.2 6.2 4.4 441.936
4.5 16 6 4.5 432
4.6 15.8 5.8 4.6 421.544
4.7 15.6 5.6 4.7 410.592
4.8 15.4 5.4 4.8 399.168
4.9 15.2 5.2 4.9 387.296
We can see from the spreadsheet that the maximum volume, of 512.864 cubic
inches will be achieved when the height is 3.1 inches. The reason that
I copied the height over by the volume was to create the following graph.
Using the different programs makes this problem fun.