#4
Consider the reduced cubic
For what values of p does the equation
have 3 real roots?
We should first look at the graph of the equation in the xp plane. Then
decide at what point could could we draw a horizontial line across the graph
and intercept the graph in three different place.
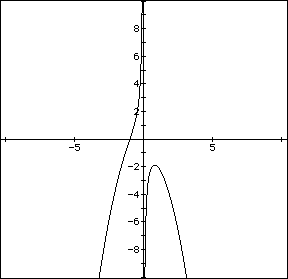
We can do this at p<-1.8. We can tell this from the following graph
of p=1.8 being graphed with the original equation
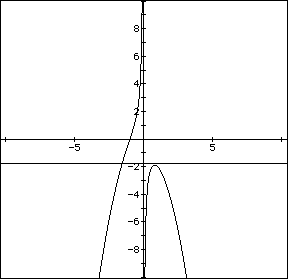
We should look at other values of q and see if we can see any patterns.
I will consider the following equations
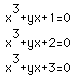
I would now like to look at their graphs
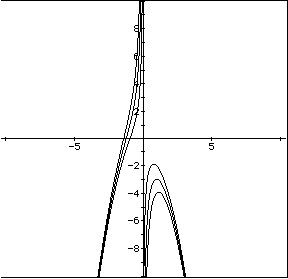
Using the same idea a before, I need to see where a horizontial line would first cross the graph in three place.
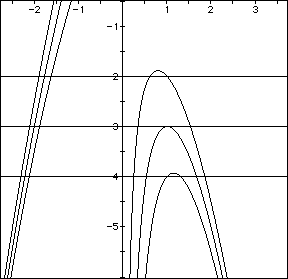
Though there is some variance, we always get three real roots at p<-(q+1)
After checking larger values, I was not satisified with this. So I made
the following t-table.
q real roots p<
1 -1.8
2 -2.9
3 -3.9
4 -4.7
5 -5.5
9 -8.1
12 -9.9
20 -14.06
34 -19.96
I also looked at a graph of thes
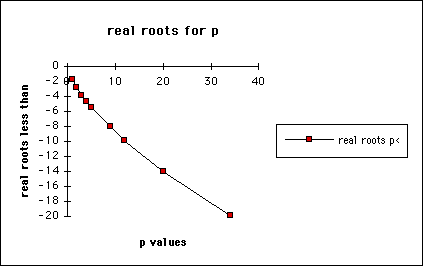
From the above graph it does not appear to be linear. So all the adding
subtracting and multipling I want to do is not going to produce my roots.
Consider the following equations
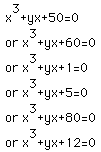
now conssider their graphs
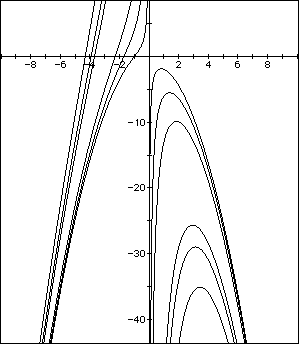
What I am looking for is some equation that will produce the maximiuns of hump part of those graphs. We would consider this to be the locuses of the points at which this equations begin to have three real roots. We must also consider that q could be negative which produces the humps in the 3rd quadrant as we will notice from the following graph.
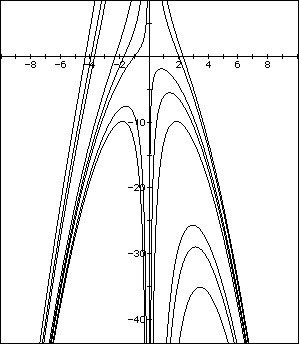
What we want is the equation that will go through the maximiums of theses
humps on both sides, or positive and negative q's if you will.
Let's consider
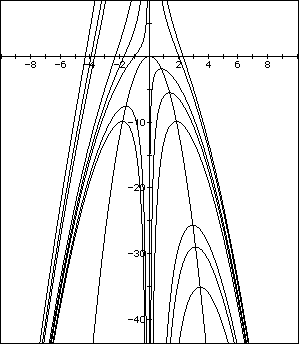
I believe that is what we are looking for. Now lets relate that to what
we are working with on the three real roots.
So what I would like ot be able to do is product an equation that will
produce the point p at which for given q that will give us three real roots.
I took some random values of q and graphed them. Then I took excell and
produced a T-table with the third column being produced by an equation to
approximate this "maximiun" value. The equation that I used was
q real roots p< three real roots
1 -1.8 -5
2 -2.9 -2.5710678
3 -3.9 -2.660254
4 -4.7 -3.25
5 -5.5 -3.9803399
9 -8.1 -7
12 -9.9 -9.0705081
20 -14.06 -13.81068
34 -19.96 -20.419465
50 -25.6 -26.535339
60 -29 -29.879833
70 -32 -32.961573
80 -35 -35.83386
100 -40.8 -41.09
130 -48.75 -48.078002
150 -53.4 -52.297244
Though some of the smaller p's are not matching up exactly, this does seem
to bee working for most of the positive values.
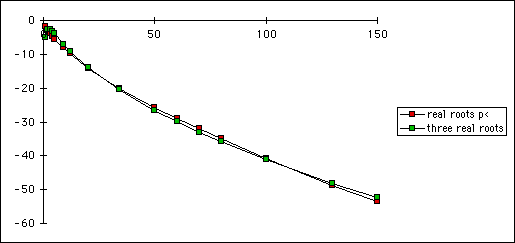
I decided to consider solving the equation
when we know that this equation is at the local maximiun which is when we have
If we do this we will get
hence;
we can plug this back into the origanal equation
So we could take any value of q and plug it in to that equation and get
the the relative maximium that we are looking for . I have taken this and
created a spreadsheet and a graph to show that it works.
q real roots p< three real roots
1 -1.8 -1.8898816
2 -2.9 -3
3 -3.9 -3.9311121
4 -4.7 -4.7622032
5 -5.5 -5.5260472
9 -8.1 -8.1770427
12 -9.9 -9.9057817
20 -14.06 -13.924767
34 -19.96 -19.834467
50 -25.6 -25.649639
60 -29 -28.964682
70 -32 -32.099624
80 -35 -35.088213
100 -40.8 -40.716264
130 -48.75 -48.498707
150 -53.4 -53.3534
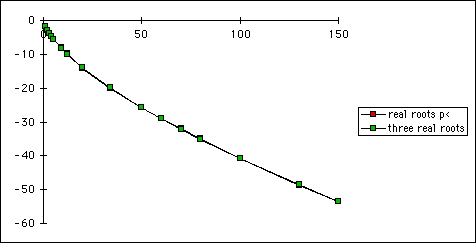
We can tell from the graph that the values created from the equation are approxiamately the same as the approximations that I had observed from using Algebra Xpressor.