
Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various
locations of P.
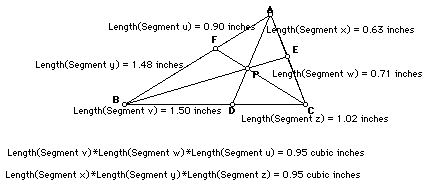
We can see from the above sketch that the two products will be the same.
I will move point P around and see if the product remains the same
The product remained the same. I noticed that the largest it will be is
1. This occurs when point P in located at the centroid.
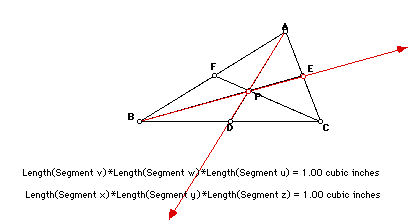
Now to prove that (CE)(AF)(BD)=(FB)(DC)(EA)
We need to really look at the ratio
The first thing that we must do is to draw a parallel line through point A that is parallel to BC
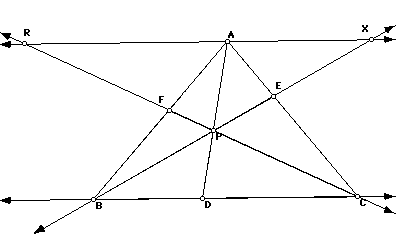
We had to extend CF to intersect the parallel line at point R,and we
had to extend BE to intersect the parallel line at point X. The reason we
needed to do this was to giove us some similiar triangles .
We get similiar triangles RAP to CDP; XAP to BDP
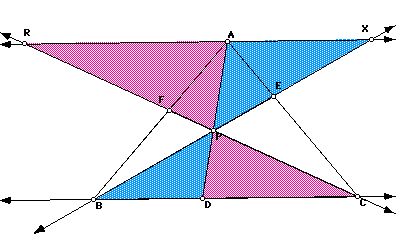
From these similiar triangles we will get one of the ratios that we need
We also got the similiar triangles XAE to BCE ; RAF to CBF
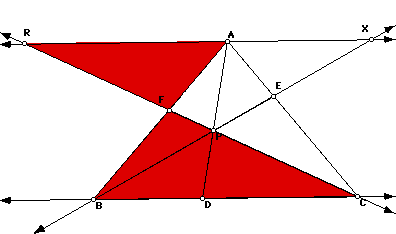
From these similiar triangles we will get
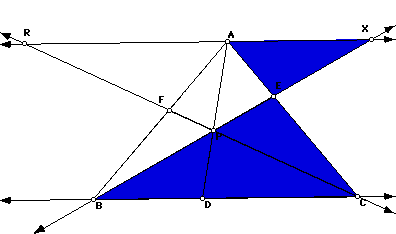
Now using these ratios, we get the following
then canceling on the right side
which will give us
Therefore we have proved that if the point is on the inside that this
will hold true. The quesiotn still can be considered if P is on the outside.
I worked with the construction and believe that is does hold to be true.