The Lidless Box

Given a rectangular sheet of cardboard 15 in. by 25 in. If a small square of the same size is cut from each corner and each side folded up along the cuts to form a lidless box.

What is the maximum volume of the box?

What size(s) of the square would produce a box of volume equal to 400 cubic inches?



Let's first try to develop some equation to represent the situation.

In this case,

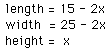
Plug these values into the equation above.

When we graph this equation in algebra xpresser, we get this picture.

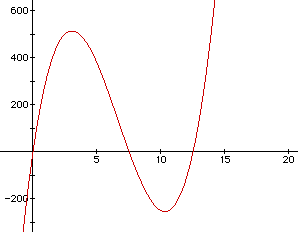
This picture gives us lots of information. First we need to know what to use from the graph. We only need the part from x = 0 to x = about 8. When x is negative, the problem does not make sense (you can't have a negative amount to remove). Now let's zoom in on the relevant part of the graph.

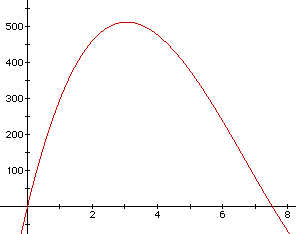
If we can find the maximum of the curve (the highest point), we will have the maximum volume on the y axis and the amount to remove from each corner on the x axis. Make some guesses and graph those lines.

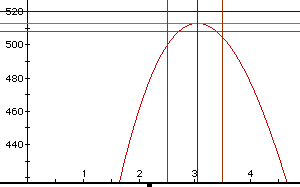
From just looking at the graph, we can conclude the volume is maximized around 513 and the part removed would equal about 3.04. These are just approximations.



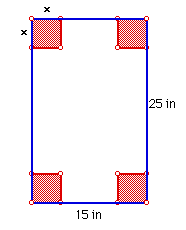
Another way to look at the problem is using GSP.

Click here to open the GSP sketch to vary the value of x.

This gives a better idea of where the components of the dimensions arise from (25 - 2x,etc.).



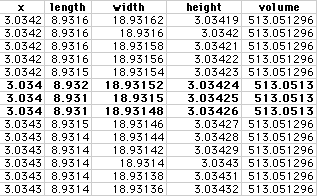
We can even use a spreadsheet to approximate values of x.

 

In this case x has increments of 0.00001. We could get an even closer approximation if we make these increments smaller. But for the purposes of the problem, they are already smaller than we would actually be able to use.



As you can see, there are many ways to present this problem depending on your resources. In an ideal situation, I would use all three. Allow students to make conjectures with one piece at a time, and not necessarily in this order. It may work better to start with a sketch in gsp, or maybe even give them the paper first, to cut from. Then show the gsp sketch that gives all possible situations, instead of just the one the originally cut. Allow them to calculate some volumes with approximations of x and then let the spreadsheet do it. See if they can form some ideas about the equation. Lastly, go to algebra expresser to show the actual graph.



If the volume is set to 400 cubic inches, let the students pick how to find x. Unless we change some calculations on our spreadsheet, we can't see exactly 400 cubic inches. Maybe it will be just as easy to go to our graph in algebra expresser.

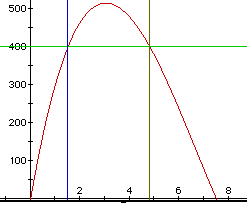
By graphing and making some approximations for x then checking them by graphing the lines, we see that at a volume of 400 cubic inches, you could cut away 1.5 inche square from each side or 4.82 inch square from each side.



Return to Sherry's class page