

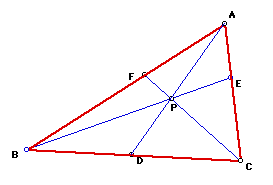
Prove the following
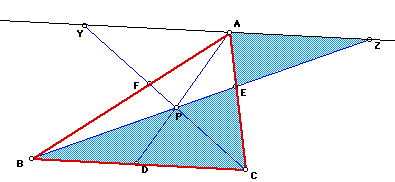
First we need to construct a parallel line to BC through A. Extend BE
to point Z and CF to Y so that Y and Z lie on this parallel line.
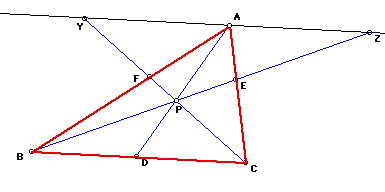
Angle APY = Angle CPD because vertical angles are congruent.
Angle AYP = Angle PCD because alternate interior angles are congruent.
Angle YAP = Angle CDP """
Triangle YAP ~ Triangle CDP by AAA.
Then
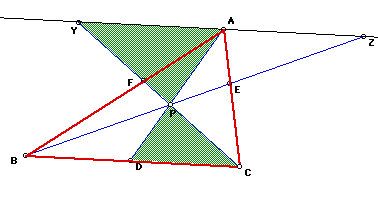
Similarly, triangle ZAP ~ triangle BDP by AAA.
Then![]()
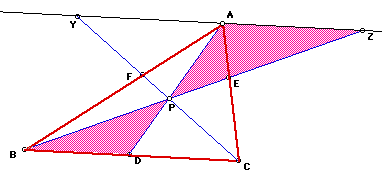
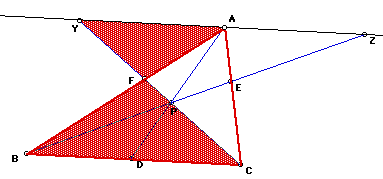
Just to make things easier to see, here are all the important ratios
together.
![]() ,
, ![]() ,
, ![]()
Since each is equal to another, let's take one side from each of the three
equalities and multiply them.
Take the other side of each of the three equalities and multiply , then
the ratios are equal.
As you can see, the right side of this equation reduces to 1.