On Pedal Triangles

I constructed a pedal triangle RST for a given triangle ABC for an arbitrary point P. For an arbitrary point P of the plane, the pedal triangle is the triangle formed by constructing perpendiculars to the sides ABC (extended if necessary):

Then I moved the point P on the circumcircle of ABC:

.

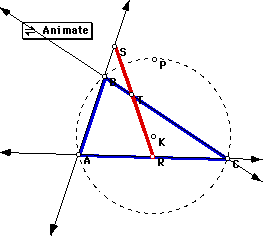Click the image to download a GSP file that contains an animation for this case. Notice that there are points on the circumcircle for which the degenerated triangle coincides with each of the sides. What is the length of the line? It must be less than or equal to the diameter of the circumcircle (obviously it can be larger!) When is the line equal to the diameter of the circumcircle? When does it have the same lenght as the sides of the triangle ABC?

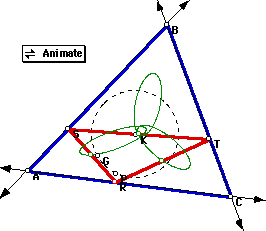
If the pedal point is inside the triangle or on the sides, the triangle RST will be inscribed in the triangle ABC; check the following animation; the pedal point P is moving along the side AB (and beyond) of the original triangle:


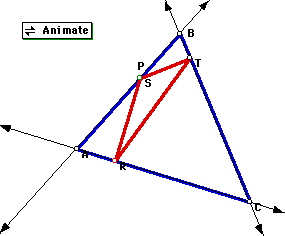
The Pedal Triangle and the Centers of the Triangle

The next figures show what is RST when P is the incenter, the circumcenter, the centroid or the orthocenter of ABC.
Incenter, I: couldn't find something special. Although the triangles seem to be similar, observe that the line trough RS is not parallel to BC. Double click to download an animation file, and check in it different triangles ABC.

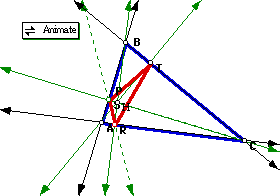
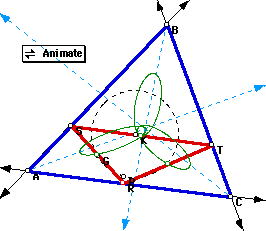
Circumcenter, K: (Double click to download an animation; check for different triangles ABC)

In any case the pedal triangle RST is similar to ABC. ST is parallel to AC, TR is parallel to AB and RS is parallel to BC. Recall that by construction K is in the intersection of the perpendicular lines to the midpoint of the sides!

Centroid, G: I couldn't find anything special. Notice that the line Sr is not parallel to the line BC. (Double click to download an animation; check for different triangles ABC

Orthocenter: Nothing special. Double click and check for different triangles ABC; What happens when H is outside ABC?

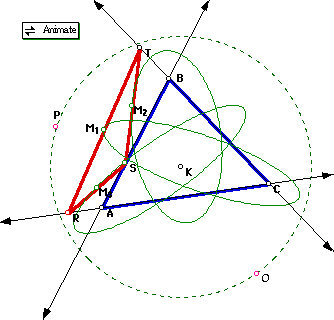
The Pedal Triangle and its Midpoints with P on a Special Circle

Tracing the midpoints of the sides of RST when the pedal point moves along a circle with center at the circumcenter and radius greater than the circumcircle, we obtain three 'ellipse' kind of curves Click here to download a file with an animation; test different triangles.

Double click the image and download a file to check for different radius and different triangles. Can you tell what the focus of the ellipses are?
We just discovered that if the circle is the circumcircle, we get a line. This is called the Simson line. The tracing of the midpoints yield again ellipses:

In this case the vertices of ABC and of RST belong to the ellipses!
If the circle has a radius less than the radius of the circumcircle we get:

We got also ellipses. But for sure you must have noticed that the ellipses are in some sense "oriented". is there any relationship between the axis ellipses and some lines of the triangle? When the circle is bigger than the circumcircle the angle bisectors correspond to the longer axis of the ellipse. This does not happen for the case in which P traces the circumcircle:

And it seems to hold also for a circle smaller than the circumcircle:

You need to take a closer look to see that this is not true!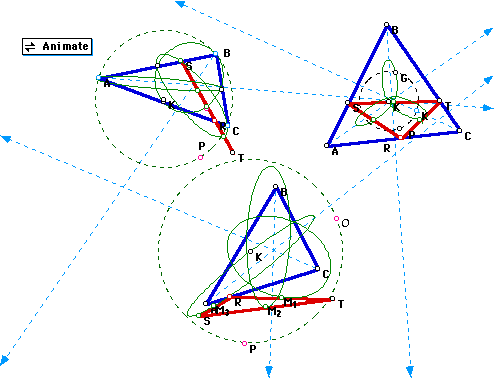

The Line Between P and the Orthocenter of ABC

Animating the pedal point on the circumcircle, and connecting P to the orthocenter, we get a new line (the pink one):

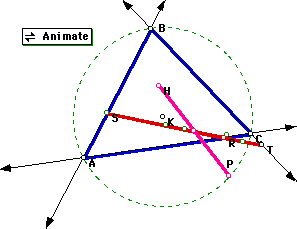
It seems that the Simson line divides the line HP in a half. But this is not true. Check in the following animation that the ratios are not (always) in proportion 2:1.

Notice that the ratio is a value very near to 2; nevertheless it is not 2, although the sum of the ratios is 4. But this is not true for ALL the cases; There are points P on the circumcircle for which the sum of ratios is greater thatn 2. Check what happens for P near the circumcenter K, or near to the vertices of ABC. Notice that more than two ratios are nedded because the Simpson line is a degenerated triangle, so it is formed by tree different lines!

So the Simson line is not divided in two equal parts.
Now consider the trace of the point of intersection between the two lines:

Notice that when the orthocenter is inside the triangle we get a circle that is tangent to one side of the triangle. When the orthocenter is outside the triangle, the circle is discontinuous. Also note that there are smal "jumps" in the circles. They correspond to the cases in which P is approaching to the vertices of the triangle. Click here is you want to download an animation and test different triangles ABC.

Back to my Home Page