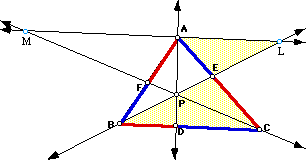
Exploration with an Interior Point a Triangle

Problem 1

Take any triangle ABC and P an interior point of it. Draw lines AP, BP, and CP extended to their intersection with the opposite sides in points D, E, and F, respectively. Explore (AF)(BD)(EC) and (FB)(DC)(EA) for various triangles and various locations of P.

The figure shows a particular case of the problem. In any case, the two expressions, (AF)(BD)(EC) and (FB)(DC)(EA) are the same; so the ratio between them is always 1. Double click the figure to download a file that shows this fact for different P's.

Why is the ratio always 1? We can write the ratio as:

So, we need to prove that the product of those ratios is 1.
Now consider the following construction:

The line ML through A is parallel to the side BC. Observe that the triangles MLP and CBP are similar and so are the pairs MAP and CDP and LAP and BDP. From this facts the following relations can be derived:

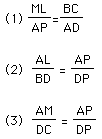
And so, from (2) and (3), we conclude:, and this combined with (1) gives:

.

the same construction shows us other pairs of similar triangles, AEL and CEB:

and AFM and BFC:

From these facts we can derive the following relations:

or

and also:

or

So combining (4), (5) and (6) we get:

Problem 2

Take any triangle ABC and P an exterior point of it. Draw lines AP, BP, and CP extended to their intersection with the opposite sides in points D, E, and F, respectively-extending the sides of the triangle if necessary. Verify that in this case the relation (AF)(BD)(EC) = (FB)(DC)(EA) also holds.
The figure shows a particular case of the problem. In any case, the two expressions, (AF)(BD)(EC) and (FB)(DC)(EA) are the same; and so, so the ratio between them is always 1. Double click the figure to download a file that shows this fact for different P's.

The same construction done before is useful for proving this fact. Notice that the triangles PBD and PJA are similar:

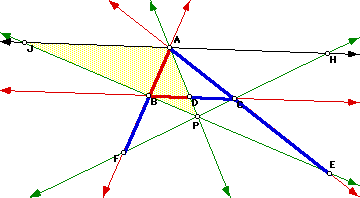
So we got . And the triangles PDC and PAH are similar, so we get: , or , so .

But also the triangles EBC and EJA are similar:

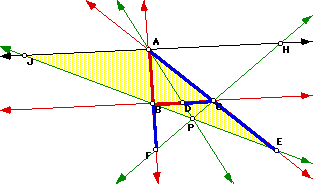
So, , or .
The triangles AFH and BFC are similar:

so we get , or .
From (1), (2) and (3), we got . So the result also holds for P outside the triangle.

Problem 3

Take any triangle ABC and P an interior point of it. Draw lines AP, BP, and CP extended to their intersection with the opposite sides in points D, E, and F, respectively. Consider the area of the triangle EFD. Show that the ratios of the areas of ABC and DEF is always greater than or equal to 4.
The figure shows a particular case of the problem. Double click on it to paly with an animation of the problem.



Notice that in the case in which the sides of DEF are parallel to the sides of ABC, we will get two similar triangles, so as P approaches to the centroid of the trianlge ABC, the ration becomes closer to 4, being four when p is the centroid. This makes sense, because the centroid is the intersection of the medians of the triangle; being each side in a ratio of 2:1, the corresponding areas are in a ratio of 2*2 = 4.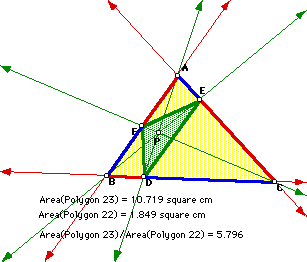

For other P's, the triangle DEF is smaller in comparison to the triangle ABC. Its area becomes zero when P is any one vertex; so dividing by a number that approaches to zero makes the ratio to grow very fast:


Back