Special Points of a Triangle, Part Two

By Vilma Mesa

Abstract

The object of this second paper is to show the results of the exploration related with the following problem:

Given any triangle ABC, construct squares externally on each side; locate the centroid of each square and join it with the oposite angles ABC. Show that the lines are concurrent and explore the relationship between the point of concurrence and the orthocenter, centroid, incenter, and circumcenter of the triangle ABC.

Some conjectures are set, some led to propositions that are proven at the end of the presentation.

Solution

In this second part I have changed the external triangles by squares:

It seems that I have again a point of concurrence:

Let's call this point T, and refer to the section Proofs to see why the lines are concurrent.
In the last exploration we analyzed if the point T was colineal with any of the Triangle Centers of the original triangle, and found that there is no colinearity relationship between T and the Triangle centers. The next table summarizes the result; the entries answer the question, Are T, the point in the row-label, and the point in the colum-label colinear?

...............................G.......... H...........K.......... I

Centroid, G............--.......... No........ No........ No
Orthocenter, H...... --............--.......... No........ No
Circumcenter, K....--............--...........--........... No

We established colinearity only in special cases, when the triangle was isoceles and equilateral.
Let's fill a new table for this new extension of the problem.

..............................G.......... H...........K.......... I

Centroid, G............--.......... __..........__......... __
Orthocenter, H...... --............--..........__......... __
Circumcenter, K....--............--...........--.......... __

The next figures show the centroid and the orthocenter, and the centroid and the circumcenter of two arbitrary triangles; observe that the line that joins each pair does not contain T.

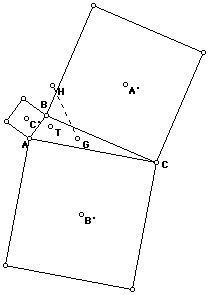
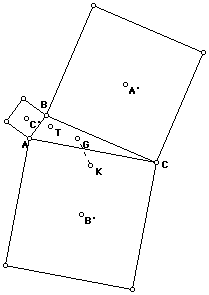
So we can fill two entries on our table:
..............................G.......... H...........K.......... I

Centroid, G............--.......... No..........No...... __
Orthocenter, H...... --............--..........__........ __
Circumcenter, K....--............--...........--......... __

Let's verify the the centroid with the incenter, and the orthocenter with the circumcenter:

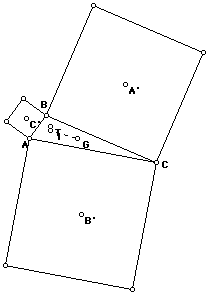
The entries on our table are now:
So we can fill two entries on our table:
..............................G.......... H...........K.......... I

Centroid, G............--.......... No..........No...... No
Orthocenter, H.......--............--...........No........ __
Circumcenter, K....--............--...........--......... __

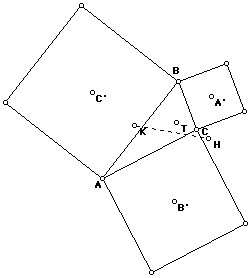
Next the orthocenter and the incenter:

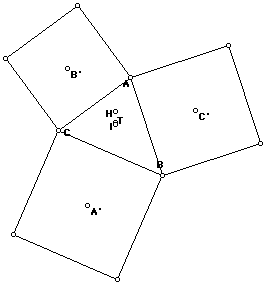
Well it seems that we are going to be able to put a Yes in the table!
The entries on our table are now, but refer to the section Proofs to see why we have a Yes:
So we can fill two entries on our table:

..............................G.......... H...........K.......... I

Centroid, G............--.......... No..........No...... No
Orthocenter, H.......--............--...........No.......Yes
Circumcenter, K....--............--...........--......... __

The last pair we need to verify is the circumcenter and the incenter:

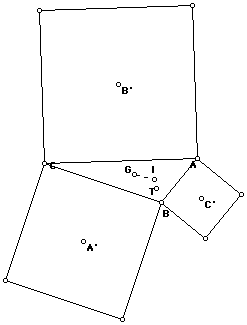
And thya re not colinear with T, so our filled table is as follows:

..............................G.......... H...........K.......... I

Centroid, G............--.......... No..........No........No
Orthocenter, H.......--............--...........No........Yes
Circumcenter, K....--............--...........--...........No

We can not say anything different if the triangle is straight:

But we can, if the triangle is isoceles:

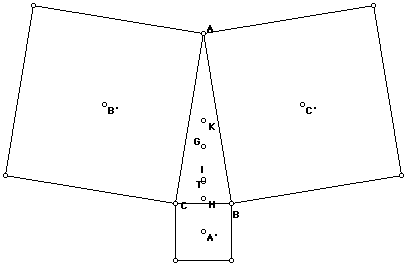
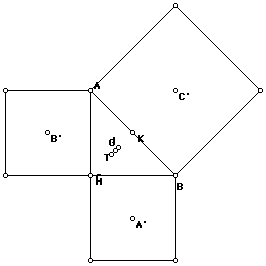
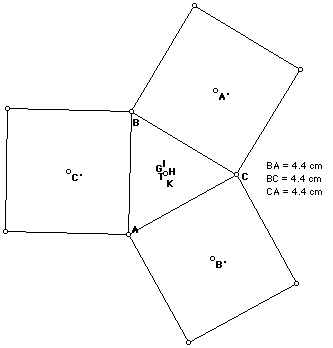
Here we two more propositions that deserve a proof!

In our next exploration, we are going to change the definition of T.

Proofs

Proposition 1

Given any triangle ABC, the lines AA', BB', and CC' that join the centroids A', B', and C' of the external squares built on each side of the triangle ABC, with the opposite angles A, B, and C respectively, are concurrent, at some point T.

Proposition 2

Given the construction of Proposition 1 on any triangle ABC, the points T, the orthocenter H and the incerter I are colinear.

Proposition 3

Given the construction of Proposition 1 on an isoceles triangle ABC, the point T is colinear with all its Triangle Centers. Moreover, if the triangle ABC is equilateral, then all these points are concurrent.

Return to my home page.